a) Rút gọn Q
b) Tính giá trị của Q tại x=4
Help me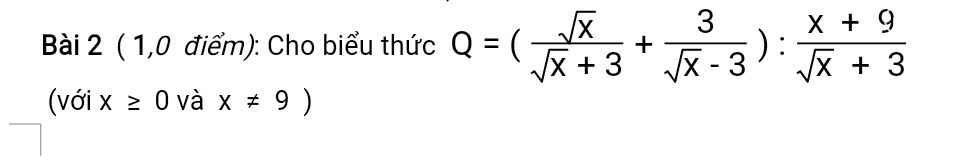
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
1
1 tháng 7 2017
\(4x^2-28x+49=\left(2x\right)^2-2\cdot2x\cdot7+7^2=\left(2x-7\right)^2\)
Khi x=4 thì \(4x^2-28x+49=\left(2x-7\right)^2=\left(2\cdot4-7\right)^2=1\)
10 tháng 3 2020
\(B=\left(\frac{2x+1}{2x-1}+\frac{4}{1-4x^2}-\frac{2x-1}{2x+1}\right):\frac{x^2+2}{2x+1}\left(x\ne\pm\frac{1}{2}\right)\)
\(\Leftrightarrow B=\left(\frac{2x+1}{2x-1}-\frac{4}{4x^2-1}-\frac{2x-1}{2x+1}\right):\frac{x^2+2}{2x+1}\)
\(\Leftrightarrow B=\left(\frac{\left(2x+1\right)^2}{\left(2x-1\right)\left(2x+1\right)}-\frac{4}{\left(2x-1\right)\left(2x+1\right)}-\frac{\left(2x-1\right)^2}{\left(2x-1\right)\left(2x+1\right)}\right)\cdot\frac{2x+1}{x^2+2}\)
\(\Leftrightarrow B=\frac{\left(2x\right)^2+2\cdot1\cdot2x+1-4-\left[\left(2x\right)^2-2\cdot2x\cdot1+1^2\right]}{\left(2x-1\right)\left(2x+1\right)}\cdot\frac{2x+1}{x^2+2}\)
\(\Leftrightarrow B=\frac{4x^2+4x-3-4x^2+4x-1}{\left(2x-1\right)\left(2x+1\right)}\cdot\frac{2x+1}{x^2+2}\)
\(\Leftrightarrow B=\frac{\left(8x-4\right)\left(2x+1\right)}{\left(2x-1\right)\left(2x+1\right)\left(x^2+2\right)}=\frac{4\left(2x-1\right)\left(2x+1\right)}{\left(2x-1\right)\left(2x+1\right)\left(x^2+2\right)}=\frac{4}{x^2+2}\)
b) \(B=\frac{4}{x^2+2}\left(x\ne\pm\frac{1}{2}\right)\)
Với x=-1 (TMĐK) thay vào B ta có:
\(B=\frac{4}{\left(-1\right)^2+2}=\frac{4}{1+2}=\frac{4}{3}\)
Vậy \(B=\frac{4}{3}\)khi x=-1
PP
27 tháng 3 2020
a) A có nghĩa khi \(\hept{2x-2\ne02-2x^2\ne0\Leftrightarrow\hept{\begin{cases}2x\ne2\\2x^2\ne2\end{cases}\Leftrightarrow}\hept{\begin{cases}x\ne1\\x\ne\pm1\end{cases}\Leftrightarrow}x\ne\pm1}\)
Vậy A có nghĩa khi \(x\ne\pm1\)
b) \(A=\frac{x}{2x-2}+\frac{x^2+1}{2-2x^2}\left(x\ne\pm1\right)\)
\(\Leftrightarrow A=\frac{x}{2\left(x-1\right)}+\frac{x^2+1}{2\left(1-x^2\right)}\)
\(\Leftrightarrow\frac{x}{2\left(x-1\right)}-\frac{x^2+1}{2\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow A=\frac{x\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}-\frac{x^2+1}{2\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow A=\frac{x^2+x-x^2+1}{2\left(x-1\right)\left(x+1\right)}=\frac{x+1}{2\left(x-1\right)\left(x+1\right)}=\frac{1}{2\left(x-1\right)}\)
Vậy A=\(\frac{1}{2\left(x-1\right)}\left(x\ne\pm1\right)\)
b) \(A=\frac{1}{2\left(x-1\right)}\left(x\ne\pm1\right)\)
A=\(\frac{-1}{2}\)\(\Leftrightarrow\frac{1}{2\left(x-1\right)}=\frac{-1}{2}\)
\(\Leftrightarrow-2\left(x-1\right)=2\)
<=> x-1=-1
<=> x=0 (tmđk)
Vậy x=0 thì \(A=\frac{-1}{2}\)
7 tháng 2 2017
a ) A = |2x - 1| - (x - 5)
Ta có : \(\left|2x-1\right|=\hept{\begin{cases}2x-1\Leftrightarrow2x-1\ge0\Rightarrow x\ge\frac{1}{2}\\-\left(2x-1\right)\Leftrightarrow2x-1< 0\Rightarrow x< \frac{1}{2}\end{cases}}\)
TH1 : 2x - 1 ≥ 0 thì A = 2x - 1 - (x - 5) = 2x - 1 - x + 5 = x + 4
TH2 : 2x - 1 < 0 thì A = - 2x + 1 - x + 5 = - 3x + 6
b ) Để A = 4 <=> x + 4 = 4 hoặc - 3x + 6 = 4
TH1 : x + 4 = 4 => x = 0
TH2 : - 3x + 6 = 4 => x = 2/3
Vậy x = { 0;2/3 } thì A = 4
7 tháng 2 2017
a, A=|2x-1|-(x-5)
A=|2x-1|-x+5
A=2x-1-x+5
A=2x-x+4
A=x+4
19 tháng 3 2020
\(A=\left|x+5\right|+2-x\)
Thay \(x=-\frac{3}{4}\)vào \(\left|x+5\right|+2-x\)ta có:
\(\left|-\frac{3}{4}+5\right|+2-\frac{-3}{4}\)
\(=\left|-\frac{3}{4}+\frac{20}{4}\right|+2-\frac{-3}{4}\)
\(=\frac{17}{4}+2+\frac{3}{4}\)
\(=\left(\frac{17}{4}+\frac{3}{4}\right)+2\)
\(=5+2\)
\(=7\)
\(Q=\dfrac{x-3\sqrt{x}+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}+3}{x+9}=\dfrac{x+9}{\left(\sqrt{x}-3\right)\left(x+9\right)}=\dfrac{1}{\sqrt{x}-3}\)
Cho mik hỏi câu nào a câu nào b ạ