Cho hàm số y = - x 3 + 3 x 2 + 2 . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên 0 ; 3 . Tính M + m
A. 8.
B. 10.
C. 6.
D. 4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Xét hàm số ![]() .
.
![]() ;
;
![]()
![]()

Bảng biến thiên

Do ![]() nên
nên ![]() suy ra
suy ra ![]() .
.
Suy ra  .
.
Nếu ![]() thì
thì ![]() ,
, ![]()
![]()
![]()
![]() .
.
Nếu ![]() thì
thì ![]() ,
, ![]()
![]()
![]()
![]() .
.
Do đó ![]() hoặc
hoặc ![]() , do a nguyên và thuộc đoạn
, do a nguyên và thuộc đoạn ![]() nên
nên ![]() .
.

+ Xét hàm số y= x4- 4x3+ 4x2+ a trên đoạn [ 0; 2].
Ta có đạo hàm y’ = 4x3-12x2+ 8x,
y
'
=
0
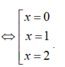
Khi đó; y( 0) = y( 2) = a; y( 1) = a+ 1
+ Nếu a≥ 0 thì M= a+ 1,m = a.
Để M ≤ 2m khi a≥ 1, suy ra a ∈ 1 ; 2 ; 3 thỏa mãn
+ Nếu a≤ - 1 thì M = a = - a , m = a + 1 = - a - 1 .
Để M≤ 2m thì a≤ -2, suy ra a a ∈ - 2 ; - 3
Vậy có 5 giá trị nguyên của a thỏa mãn yêu cầu.
Chọn B.

Chọn D
Ta có 3x.f(x) -
x
2
f
'
(
x
)
=
2
f
2
(
x
)
![]()
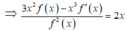
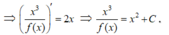
Thay x = 1 vào ta được 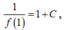 vì f(1) =
1
3
nên suy ra C = 2
vì f(1) =
1
3
nên suy ra C = 2
Nên  Ta có:
Ta có: 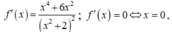
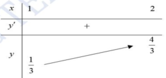
Khi đó, f(x) đồng biến trên [1;2]
Suy ra ![]()
Suy ra ![]()

Đáp án D
Ta có ![]() liên tục trên đoạn
liên tục trên đoạn ![]() .
.
Ta có ![]()
 .
.
![]() .
.
Vậy m=2 và M = 11, do đó ![]() .
.

Đặt y= f(x) = \(x^2-2\left(m+\dfrac{1}{m}\right)x+m\)
Hoành độ đỉnh của đồ thị hàm số x=\(m+\dfrac{1}{m}\ge2\) (BĐT co-si)
vì hệ số a =1>0 nên hàm số nghịch biến trên \(\left(-\infty;m+\dfrac{1}{m}\right)\)
Suy ra, hàm số nghịch biến trên \(\left[-1;1\right]\)
=> y1 = f(-1) = \(3m+\dfrac{2}{m}+1\)
y2 = f(1)=\(1-m-\dfrac{2}{m}\)
theo đề bài ta có : y1-y2=8 <=> \(3m+\dfrac{2}{m}+1-1+m+\dfrac{2}{m}=8\left(m>0\right)\)
<=> \(m^2-2m+1=0\)
<=> m=1
Đáp án là A