Cho tam giác ABC có tọa độ 3 đỉnh A(2;0), B(-2;4) và C(3;2).Tìm tọa độ N∈ x'Ox sao cho tứ giác ABNC là hình thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
3 tháng 6 2023
Đối xứng của A qua trục tung là A'(4; -1) và đối xứng của A qua trục hoành là A"(-4; 1).
Vậy đỉnh thứ hai của tam giác cân là I(-4; -1).
Ta có thể tính được hệ số góc của đường thẳng AI bằng công thức:
\(m=\dfrac{y_A-y_I}{x_A-x_I}=\dfrac{1-\left(-1\right)}{4-\left(-4\right)}=\dfrac{1}{4}\)
Vậy phương trình đường thẳng AI là:
\(y-y_A=m\left(x-x_A\right)\)
\(y-1=\dfrac{1}{4}\left(x-4\right)\)
\(4y-4=x-4\)
\(x-4y=0\)
Vậy phương trình đường thẳng cần tìm là \(x-4y=0\)
H
3 tháng 6 2023
Đường thẳng đi qua A và tạo với hai trục tọa độ một tam giác cân đỉnh là gốc tọa độ sẽ qua điểm trung điểm của đoạn thẳng BC, ký hiệu là M.
Có:
Tọa độ x của trung điểm M = \(\dfrac{x_B+x_C}{2}=\dfrac{3+1}{2}=2\)
Tọa độ y của trung điểm M = \(\dfrac{y_B+y_C}{2}=\dfrac{2+6}{2}=4\)
Vậy tọa độ của điểm M là (2, 4).
Phương trình đường thẳng đi qua A và M là:
\(y-1=\dfrac{4-1}{2-4}.\left(x-4\right)\Rightarrow y=-1,5x+7\)y
Vậy phương trình đường thẳng cần tìm là \(y=-1,5x+7.\)
(Cái câu kia mình làm cho bài khác tính cop màn hình mà bấm gửi nhầm ở đây, bài giải này mới đúng nhé!)
CM
6 tháng 6 2018
Chọn A.
Gọi tọa độ điểm C( x ; y)
Vì O là trọng tâm tam giác ABC nên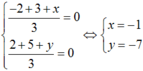 
22 tháng 3 2017
A B C M N E H
goi B(a; b) N( c; d)
\(N\in\left(CN\right)\Rightarrow\)c+8d-7 = 0(1)
N la trung diem AB\(\Rightarrow2c=1+a\left(2\right)\)
2d = -3 +b (3)
B\(\in\left(BM\right)\)\(\Rightarrow\)a+b -2 =0 (4)
tu (1) (2) (3) (4) \(\Rightarrow a=-5;b=7\Rightarrow B\left(-5;7\right)\)
dt (AE) qua vuong goc BM. \(\Rightarrow pt\)(AE):x-y-4 = 0
tọa độ H \(\left\{{}\begin{matrix}x-y-4=0\\x+y-2=0\end{matrix}\right.\Rightarrow H\left(3;-1\right)\);H là trung điểm AE
\(\Rightarrow E\left(5;1\right)\). vì ptdt (BE) cung la ptdt qua (BC):
3x+5y-20 =0
tọa độ C là nghiệm hệ \(\left\{{}\begin{matrix}3x+5y-20=0\\x+8y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{139}{21}\\\dfrac{1}{21}\end{matrix}\right.\)
\(\Rightarrow C\left(\dfrac{139}{21};\dfrac{1}{21}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý
