Cho hàm số y = f(x) liên tục trên
ℝ
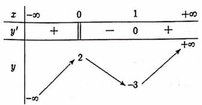
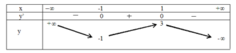
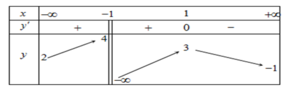
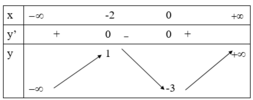
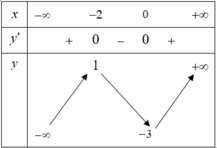
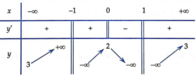
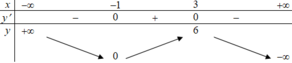
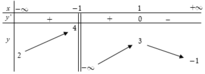
và có bảng biến thiên như hình dưới đây:
Khẳng định nào sau đây là sai?
A. Hàm số nghịch biến trên khoảng - ∞ ; - 1
B. Hàm số nghịch biến trên khoảng 1 ; + ∞
C. Hàm số đồng biến trên khoảng - 1 ; 1
D. Hàm số đồng biến trên khoảng - 1 ; 3




Đáp án là D