Tiếp tuyến của đồ thị hàm số y = x 3 − 3 x 2 − 2 có hệ số góc k=-3 có phương trình là:
A. y = − 3 x − 7
B. y = − 3 x + 7
C. y = − 3 x + 1
D. y = − 3 x − 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm
Ta có: y' \(=\dfrac{-3}{\left(x+1\right)^2}\)
k=f'\(\left(x_0\right)\)\(\Rightarrow-3=\dfrac{-3}{\left(x_0+1\right)^2}\Leftrightarrow\left(x_0+1\right)^2=1\)\(\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-2\end{matrix}\right.\)
Với \(x_0=0\) ta có pt tiếp tuyến:
\(d:3x+y-2=0\)
Với \(x_0=-2\) ta có pt tiếp tuyến:
\(d:3x+y+10=0\)
a: Tọa độ giao điểm của (d) với trục Ox là:
y=0 và (-x+2)=0
=>x=2 và y=0
\(y'=\dfrac{\left(-x+2\right)'\left(x+1\right)-\left(-x+2\right)\left(x+1\right)'}{\left(x+1\right)^2}\)
\(=\dfrac{\left(-\left(x+1\right)+x-2\right)}{\left(x+1\right)^2}=\dfrac{-3}{\left(x+1\right)^2}\)
Khi x=2 thì y'=-3/(2+1)^2=-3/9=-1/3
y-f(x0)=f'(x0)(x-x0)
=>y-0=-1/3(x-2)
=>y=-1/3x+2/3
b: Tọa độ giao của (d) với trục Oy là;
x=0 và y=(-0+2)/(0+1)=2
Khi x=0 thì \(y'=\dfrac{-3}{\left(0+1\right)^2}=-3\)
y-f(x0)=f'(x0)(x-x0)
=>y-2=-3(x-0)
=>y=-3x+2

a: y'=3x^2-6
f(1)=1-6+5=0
f'(1)=3-6=-3
y-f(1)=f'(1)(x-1)
=>y-0=-3(x-1)
=>y=-3x+3
b: y=5
=>x^3-6x=0
=>x=0 hoặc x=căn 6 hoặc x=-6
TH1: x=0
y=5; y'=3*0^2-6=-6
Phương trình sẽ là:
y-5=-6(x-0)
=>y=-6x+5
TH2: x=căn 6
y=5; y'=3*6-6=12
Phương trình sẽ là:
y-5=12(x-căn 6)
=>y=12x-12căn 6+5
TH3: x=-căn 6
y=5; y'=12
Phương trình sẽ là:
y-5=12(x+căn 6)
=>y=12x+12căn 6+5

a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)

\(y'=\left(x^3-3x^2+4x-1\right)'=3x^2-3\cdot2x+4\)
\(=3x^2-6x+3+1=3\left(x-1\right)^2+1>=1\)
Dấu = xảy ra khi x=1
=>Chọn A

- Gọi M ( x 0 ; y 0 ) là tọa độ tiếp điểm.
- Ta có:
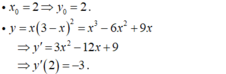
- Vậy phương trình tiếp tuyến cần tìm là :
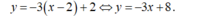
Chọn A

- Gọi M ( x 0 ; y 0 ) là tọa độ tiếp điểm.
- Ta có :
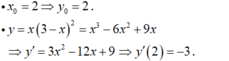
- Vậy phương trình tiếp tuyến cần tìm là
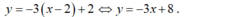
Chọn A.
Đáp án C
Ta có:
y ' = 3 x 2 − 6 x ⇒ y ' ( x ) = − 3 ⇔ 3 x 2 − 6 x + 3 = 0 ⇔ x = 1 ⇒ y = − 2