Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
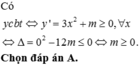
a/ Để hàm số đồng biến khi x>0
\(\Leftrightarrow1-2m>0\Rightarrow m< \frac{1}{2}\)
b/ Để hàm số nghịch biến khi x>0
\(\Leftrightarrow4m^2-9< 0\Leftrightarrow-\frac{3}{2}< m< \frac{3}{2}\)
c/ Để hàm số đồng biến khi x<0
\(\Leftrightarrow m^2-3m< 0\Leftrightarrow0< m< 3\)
d/ Do \(m^2-2m+3=\left(m-1\right)^2+2>0\) ;\(\forall m\)
\(\Rightarrow\) Hàm số đồng biến khi x>0 với mọi m
đồng biến khi a=(2m+3) >0
nghịch biến khi a=(2m+3) <0
rồi tính ra là ra m
đúng ko ạ
a) khi x>0
để đồng biến thì m+2>=0=>m>=-2
b)khi x<0
để nghịch biến thì m+2<0=>m<-2
tự trình bày nha
Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^
TH1: Lấy \(x_1;x_2\in R\) sao cho \(0< x_1< x_2\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\cdot\left(x_1^2-x_2^2\right)}{x_1-x_2}=a\cdot\left(x_1+x_2\right)\)>0 vì \(x_1+x_2>0;a>0\)
=>Hàm số y=f(x)=ax2 đồng biến khi x>0 nếu a>0
TH2: Lấy \(x_1;x_2\in R^+;0< x_1< x_2\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\cdot\left(x_1^2-x_2^2\right)}{x_1-x_2}=\dfrac{a\left(x_1-x_2\right)\left(x_1+x_2\right)}{x_1-x_2}\)
\(=a\left(x_1+x_2\right)< 0\)(vì x1+x2>0 và a<0)
=>Hàm số nghịch biến khi x>0
TH3: Lấy \(x_1;x_2\in R^-\) sao cho \(x_1< x_2< 0\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\left(x_1^2-x_2^2\right)}{x_1-x_2}=\dfrac{a\left(x_1+x_2\right)\left(x_1-x_2\right)}{x_1-x_2}\)
\(=a\left(x_1+x_2\right)>0\) vì a<0 và x1+x2<0
=>Hàm số đồng biến khi x<0
Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.
