Cho hình phẳng (H) được giới hạn bởi elip có phương trình x 2 25 + y 2 16 = 1 Tính thể tích của khối tròn xoay thu được khi quay hình phẳng (H) quanh trục Ox
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


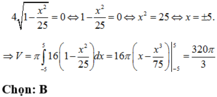

Đáp án B
Cho hai hàm số y=f(x)và y=g(x) liên tục trên [a;b] Khi đó thể tích vật tròn xoay giới hạn bởi hai đồ thị hàm số y=f(x)và y=g(x) và hai đường thẳng x=a; x=b khi quay quanh trục Ox là:
V = π ∫ a b f 2 ( x ) - g 2 ( x ) dx
Cách giải:
Ta có:
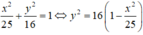
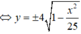
Do tính đối xứng của (H) qua Ox nên thể tích khối tròn xoay cần tìm bằng thể tích khối tròn xoay sinh ra khi quay (H') quanh Ox, trong đó (H') là hình phẳng giới hạn bởi đồ thị hàm số y = 4 1 - x 2 25 và trục Ox.
Xét phương trình hoành độ giao điểm
4 1 - x 2 25 = 0 ⇔ 1 - x 2 25 = 0 ⇔ x 2 = 25 ⇔ x = ± 5
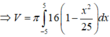
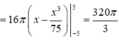

Tìm hoành độ giao điểm của hai dồ thị, ta có:
( x - 1 ) e 2 x = 0 => x = 1
Vậy thể tích của khối tròn xoay thu được khi quay (H) quanh Ox được tính bởi
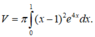
Đặt: u = ( x - 1 ) 2 , d v e 4 x d x . Ta có du = 2(x -1)dx và v = e 4 x 4 .
Áp dụng công thức tích phân từng phần ta được
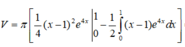
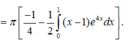
Đặt u 1 = x - 1 , d v 1 = e 4 x d x , ta có d u 1 = d x , v 1 = e 4 x 4
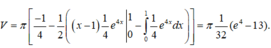
Vậy chọn đáp án A.