Cho hàm số f ( x ) = 1 x 2 1 - x 2 Tìm nguyên hàm của hàm số g ( t ) = c o s t . f ( sin t ) , với t ∈ ( - π 2 ; π 2 ) ∖ { 0 } là
A. F(t)=-tant+C
B. F(t)=-cott+C
C. F(t)=tant+C
D. F(t)=cott+C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

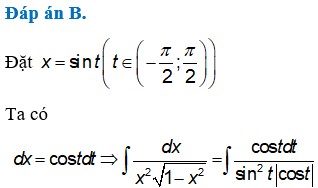
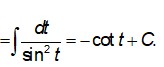

Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Bài 2:
Lần lượt thay các giá trị của x, ta có:
_Y=f(-2)=-2.(-2)+3=7
_Y=f(-1)=-2.(-1)+3=1
_Y=f(0)=-2.0+3=3
_Y=f(-1/2)=-2.(-1/2)+3=4
_Y=f(1/2)=-2.1/2+3=2

Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.