Cho hình chóp S.ABC có mặt bên SAB vuông góc với mặt phẳng đáy, tam giác SAB đều cạnh a, tam giác BAC vuông cân tại A. Tính khoảng cách h giữa hai đường thẳng AB và SC.
A. h = a . 3 7
B. h = a . 3 7
C. h = a . 7 3
D. h = a . 7 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp giải: Dựng hình, xác định khoảng cách giữa hai đường thẳng thông qua mặt phẳng song song với đường thẳng
Lời giải:


Đáp án A
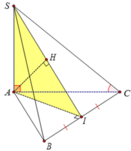
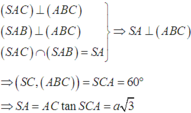
Gọi I,H lần lượt là hình chiếu vuông góc của A trên BC, SI, khi đó: d(A, (SBC)) =AH
Tam giác ABC đều cạnh a nên AI = a 3 2
Khi đó xét tam giác SAI :
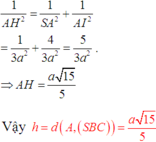
Đáp án A
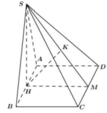
Dựng điểm D sao cho ABCD là hình vuông khi đó:
AB song song với (SDC)
=> khoảng cách giữa AB và SC
Bằng khoảng cách giữa AB và (SDC)
Gọi M,N lần lượt là trung điểm AB và DC ta có MN song song với AC nên MN vuông góc với AB. mà
SM vuông góc với AB nên AB vuông góc với (SMN). Do CD song song với AB nên CD vuông góc với (SMN) suy ra (SDC) vuông góc với (SMN)
Vì SN là giao tuyến của hai mặt phẳng trên => Kẻ MH vuông góc với SN thì MH là khoảng cách cần tìm.