Cho cấp số cộng u n với số hạng đầu u 1 = 2 và số hạng thứ năm u 5 = 14 . Tổng của 10 số hạng đầu của cấp số cộng u n là
A. 232
B. 126
C. 155
D. 187
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77

\(\left\{{}\begin{matrix}u_{14}=u_1+13d=18\\u_4=u_1+3d=-12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}d=3\\u_1=-21\end{matrix}\right.\)
Tổng 16 số hạng đầu tiên:
\(S_{16}=\frac{16\left(2u_1+15d\right)}{2}=24\)

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
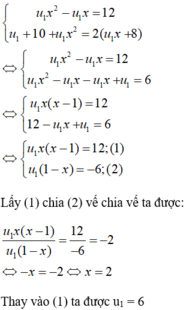
+ Tổng của năm số hạng đầu của CSN là:


Đáp án C
Gọi số hạng đầu và công sai u 1 , d ta có S n = n 2 2 u 1 + n - 1 d = 3 n 2 + 4 n
⇒ 2 u 1 - d + n d = 8 + 6 n ⇒ 2 u 1 - d = 8 d = 6 ⇒ u 1 = 7 d = 6 ⇒ u 10 = 61 .

Chọn B
Ta có: S n = 3 n 2 + 4 n = n ( 7 + 6 n + 1 ) 2
⇒ u n = 6 n + 1 ⇒ u 10 = 61
Đáp án C