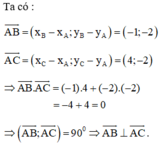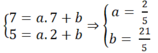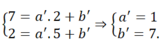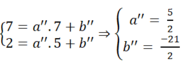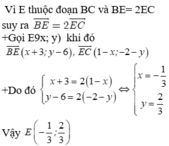Trên mặt phẳng tọa độ Oxy cho ba điểm A(a; 0); B(0; b) (với a > 0, b > 0) và C(1; 2) như trên hình 12.
a) Viết phương trình đường thẳng đi qua hai điểm A, B.
b) Tìm hệ thức liên hệ giữa a, b sao cho ba điểm A, B, C thẳng hàng.
c) Tìm các giá trị của a, b sai cho bao điểm A, B, C thẳng hàng và diện tích tam giác OAB nhỏ nhất.