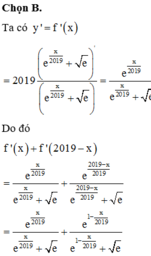
Cho hàm số y = f ( x ) = 2019 l n e x 2019 e . Tính giá trị biểu thức A = f ’ ( 1 ) ...

PT

Pham Trong Bach

22 tháng 12 2018

Cho hàm số y = f ( x ) = 2019 l n e x 2019 + e . Tính giá trị biểu thức A = f ’ ( 1 ) + f ’ ( 2 ) + … + f ’ ( 2018 ) A. 2018 B. 1009 C. 2017 2 D. 2019 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

22 tháng 12 2018

Đúng(0)

PT

Pham Trong Bach

10 tháng 2 2019

Cho hàm số y=f(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) = (3x2+2x)e-f(x) ∀ x ∈ - 1 ; 0 Tính giá trị biểu thức A=f(0)-f(-1) ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

10 tháng 2 2019

Đúng(0)

PT

Pham Trong Bach

2 tháng 4 2018

Cho hàm số f(x) là một nguyên hàm của hàm số y = e x x ≥ 1 e - x x ≤ 1 với f(1)=e. Giá trị biểu thức f(-ln⁡3)+f(-ln⁡2)+f(ln⁡2)+f(ln⁡3) bằng A. 2 e + 1 e B. 3 e + 1 e - 10 3 C. 3 e + 1 e - 5 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

2 tháng 4 2018

Đúng(0)

NT

Nguyễn Thanh

1 tháng 6 2019

Câu 1: Cho x, y là các số thực lớn hơn1 sao cho \(y^x.\left(e^x\right)^{e^y}\ge x^y.(e^y)^{e^x}\). Tìm giá trị nhỏ nhất của biểu thức p = \(log_x\sqrt{xy}+log_yx\) Câu 2 Cho hàm số y = f(x) xác định trên R\{1} có đọa hàm y' = \(\frac{1}{x-1}\), Biết f(0) = 2018, f(2) =2019. Tính S= f(3) -...

Đọc tiếp

#Toán lớp 12

2

NV

Nguyễn Việt Lâm

Giáo viên

3 tháng 6 2019

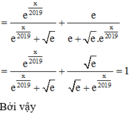
Câu 1:

Lấy logarit cơ số tự nhiên 2 vế:

\(x.lny+e^y.x\ge y.lnx+y.e^x\)

\(\Leftrightarrow\frac{lny+e^y}{y}\ge\frac{lnx+e^x}{x}\)

Xét hàm \(f\left(t\right)=\frac{lnt+e^t}{t}\) với \(t>1\)

\(f'\left(t\right)=\frac{\left(e^t+\frac{1}{t}\right).t-lnt-e^t}{t^2}=\frac{t.e^t+1-e^t-lnt}{t^2}\)

Xét \(g\left(t\right)=t.e^t+1-e^t-lnt\Rightarrow g'\left(t\right)=e^t+t.e^t-e^t-\frac{1}{t}\)

\(g'\left(t\right)=t.e^t-\frac{1}{t}=\frac{t^2.e^t-1}{t}>0\) \(\forall t>1\)

\(\Rightarrow g\left(t\right)\) đồng biến \(\Rightarrow g\left(t\right)>g\left(1\right)=1>0\) \(\forall t>1\)

\(\Rightarrow f'\left(t\right)=\frac{g\left(t\right)}{t^2}>0\Rightarrow f\left(t\right)\) đồng biến

\(\Rightarrow f\left(t_1\right)\ge f\left(t_2\right)\Leftrightarrow t_1\ge t_2\)

\(\Rightarrow f\left(y\right)\ge f\left(x\right)\Leftrightarrow y\ge x\) \(\Rightarrow log_xy\ge1>0\)

\(P=log_x\left(xy\right)^{\frac{1}{2}}+log_yx=\frac{1}{2}\left(1+log_xy\right)+\frac{1}{log_xy}\)

\(P=\frac{1}{2}+\frac{1}{2}log_xy+\frac{1}{log_xy}\ge\frac{1}{2}+2\sqrt{\frac{log_xy}{2log_xy}}=\frac{1}{2}+\sqrt{2}\)

Đúng(0)

NV

Nguyễn Việt Lâm

Giáo viên

3 tháng 6 2019

\(f'\left(x\right)=\frac{1}{x-1}\Rightarrow\int f'\left(x\right)dx=\int\frac{1}{x-1}dx\)

\(\Rightarrow f\left(x\right)=ln\left|x-1\right|+C\)

\(\Rightarrow f\left(x\right)=\left\{{}\begin{matrix}ln\left|x-1\right|+C_1\left(x>1\right)\\ln\left|x-1\right|+C_2\left(x< 1\right)\end{matrix}\right.\)

\(f\left(0\right)=2018\Leftrightarrow2018=ln\left|0-1\right|+C_2\Rightarrow C_2=2018\)

\(f\left(2\right)=2019\Rightarrow2019=ln\left|2-1\right|+C_1\Rightarrow C_1=2019\)

\(\Rightarrow f\left(x\right)=\left\{{}\begin{matrix}ln\left|x-1\right|+2019\left(x>1\right)\\ln\left|x-1\right|+2018\left(x< 1\right)\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}f\left(3\right)=2019+ln2\\f\left(-1\right)=2018+ln2\end{matrix}\right.\) \(\Rightarrow S=1\)

Đúng(0)

TQ

THI QUYNH HOA BUI

13 tháng 10 2021

Cho đa thức: f(x)= x^3/1-3x+3x^2

a) cm: f(x) + f(1-x)=1

b) Tính giá trị biểu thức: P= f(1/2021)+f(2/2021)+...+f(2019/2021)+ f(2020/2021)

#Toán lớp 8

0