Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
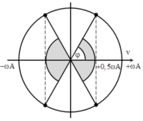
Vận tốc cực đại của con lắc v max = ωA.
+ Khoảng thời gian trong một chu kì mà tốc độ của vật nhỏ không nhỏ hơn 0,5 v max ứng với các góc quét được đánh dấu như hình vẽ.
→ Khoảng thời gian tương ứng là:
Δt = T 360 0 4 arccos 0 , 5 ωA ωA = 2 T 3
Đáp án A
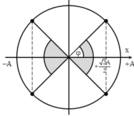
+ Khoảng thời gian trong một chu kì mà li độ của vật có độ lớn không nhỏ hơn 2 2 A ứng với các góc quét được đánh dấu như hình vẽ.
→ Khoảng thời gian tương ứng là:
Δt = T 360 0 4 arcos 2 A 2 A = T 2
Để tìm tần số dao động của con lắc, ta có công thức:
f = 1/T
Trong đó: f là tần số dao động (Hz) T là chu kì dao động (s)
Theo đề bài, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s là T/3. Độ lớn gia tốc của con lắc được tính bằng công thức:
a = -ω²x
Trong đó: a là gia tốc (cm/s²) ω là góc tốc độ góc của con lắc (rad/s) x là biên độ dao động (cm)
Ta có thể tính được ω bằng công thức:
ω = 2πf
Thay vào công thức gia tốc, ta có:
a = -(2πf)²x = -4π²f²x
Đề bài cho biết gia tốc không vượt quá 100 cm/s, nên ta có:
100 ≥ 4π²f²x
Với x = 5 cm, ta có:
100 ≥ 4π²f²(5)
Simplifying the equation:
5 ≥ π²f²
Từ đó ta có:
f² ≤ 5/π²
f ≤ √(5/π²)
f ≤ √(5/π²) ≈ 0.798 Hz
Vậy tần số dao động của con lắc là khoảng 0.798 Hz.
Đáp án D
Khoảng thời gian gia tốc có độ lớn không quá 1 m/s2 là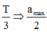 
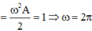rad/s → f = 1 Hz
Đáp án A
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Theo đề bài ta có
Biểu diễn trên đường tròn lượng giác ta có :
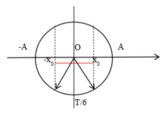
Từ đường tròn lượng giác ta thấy phần gạch đỏ là phần thỏa mãn yên cầu của đề bài => x0 = A/2 = 2,5 cm
Do đó ta có :
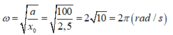
=> Tần số f = ω / 2 π => Chọn A
Đáp án B