Help thật
Bài 4: Cho hàm số . Xác định giá trị của tham số m để:
a. y' ≤ 0, ∀ x∈
b. y' = 0 có hai nghiệm phân biệt cùng âm.
c. y' = 0 có hai nghiệm phân biệt thỏa mãn điều kiện x12 + x22 = 3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình có hai nghiệm phân biệt x1, x2 ⇔ ∆ = 52 – 4(3m + 1) > 0 ⇔ 21 – 12m > 0
ó m < 21/12
Với m < 21/12 , ta có hệ thức x 1 + x 2 = 5 x 1 x 2 = 3 m + 1 V i e t '
⇒ | x 1 − x 2 | = ( x 1 − x 2 ) 2 = ( x 1 + x 2 ) 2 − 4 x 1 x 2 = 5 2 − 4 ( 3 m + 1 ) = 21 − 12 m = > | x 1 2 − x 2 2 | = | ( x 1 + x 2 ) ( x 1 − x 2 ) | = | 5 ( x 1 − x 2 ) | = 5 | x 1 − x 2 | = 5 21 − 12 m
Ta có: | x 1 2 − x 2 2 | = 15 ⇔ 5 21 − 12 m = 15 ⇔ 21 − 12 m = 3 ⇔ 21 − 12 m = 9 ⇔ 12 m = 12 ⇔ m = 1 (t/m)
Vậy m = 1 là giá trị cần tìm

bài 1 là mình đặt x = 0 rồi y = 0 nhé, đặt số nào cũng được nha nhưng mình chọn số 0 vì nó dễ :v nên mn đừng thắc mắc nhá
Bài 2 :
Để pt có 2 nghiệm pb nên \(\Delta>0\)hay
\(\left(1-m\right)^2-4\left(-m\right)=m^2-2m+1+4m=\left(m+1\right)^2>0\)
\(\Leftrightarrow m>-1\)
Theo Vi et \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=m-1\\x_1x_2=\frac{c}{a}=-m\end{cases}}\)
Ta có : \(x_1\left(5-x_2\right)\ge5\left(3-x_2\right)-36\Leftrightarrow5x_1-x_1x_2\ge15-5x_2-36\)
\(\Leftrightarrow5\left(x_1+x_2\right)-x_1x_2\ge-21\Leftrightarrow5m-5+m\ge-21\)
\(\Leftrightarrow6m\ge-16\Leftrightarrow m\ge-\frac{8}{3}\)kết hợp với đk vậy \(m>-1\)

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
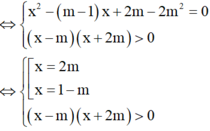
Điều kiện để pt đã cho có 2 nghiệm
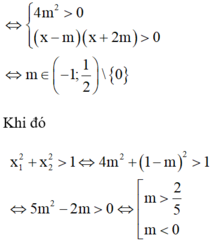
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Chọn D.
Phương trình ![]()
Ta thấy 1 - (m + 3) + m + 2 = 0 nên 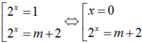
Từ đó 2x = m + 2 cần phải có nghiệm thực khác 0 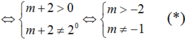
Khi đó 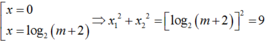
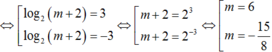 thỏa mãn (*)
thỏa mãn (*)
Kết hợp với m > 0 đề bài cho thì ta được m = 6 thỏa mãn.

Để pt có hai nghiệm pb:
\(\Leftrightarrow\)\(\Delta=16-4\left(m-4\right)>0\)\(\Leftrightarrow8>m\)
Có\(\left(x_1-1\right)\left(x_2^2-3x_2+m-3\right)=-2\)
\(\Leftrightarrow\left(x_1-1\right)\left(x^2_2-4x_2+m-4\right)+\left(x_1-1\right)\left(x_2+1\right)=-2\)
\(\Leftrightarrow x_1x_2+x_1-x_2-1=-2\) (*) (vì x2 là một nghiệm của pt nên \(x_2^2-4x_2+m-4=0\))
TH1: \(x_1>x_2\)
(*)\(\Leftrightarrow x_1x_2+\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}+1=0\)
\(\Leftrightarrow m-4+\sqrt{4^2-4\left(m-4\right)}+1=0\)
\(\Leftrightarrow\sqrt{32-4m}=3-m\) \(\Leftrightarrow\left\{{}\begin{matrix}32-4m=9-6m+m^2\\m\le3\end{matrix}\right.\) \(\Leftrightarrow m=1-2\sqrt{6}\)
TH2:\(x_1< x_2\)
(*)\(\Leftrightarrow\)\(x_1x_2-\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}+1=0\)
\(\Leftrightarrow m-4+1=\sqrt{32-4m}\) \(\Leftrightarrow\left\{{}\begin{matrix}m-3\ge0\\\left(m-3\right)^2=32-4m\end{matrix}\right.\)\(\Leftrightarrow m=1+2\sqrt{6}\) (tm đk m<8)
Vậy \(\left[{}\begin{matrix}m=1-2\sqrt{6}\\m=1+2\sqrt{6}\end{matrix}\right.\)
giải thích cho mình vì sao biến đổi đc từ
m−4+√42−4(m−4)+1 thành √32−4m
\(y=-\frac{1}{3}mx^3+\left(m-1\right)x^2-mx+3\)
\(y'=-mx^2+2\left(m-1\right)x-m\)
Với \(m=0\): \(y'=-2x\)không thỏa mãn.
Với \(m\ne0\):
\(y'\le0,\forall x\inℝ\)khi:
\(\hept{\begin{cases}-m< 0\\\Delta'=\left(m-1\right)^2-m^2\le0\end{cases}}\Leftrightarrow m\ge\frac{1}{2}\).
\(y'=0\)có hai nghiệm phân biệt cùng âm khi:
\(\hept{\begin{cases}\Delta'=-2m+1>0\\\frac{2\left(m-1\right)}{m}< 0\\\frac{-m}{-m}>0\end{cases}}\Leftrightarrow0< m< \frac{1}{2}\).
\(y'=0\)có hai nghiệm phân biệt khi \(-2m+1>0\Leftrightarrow m< \frac{1}{2}\).
\(\hept{\begin{cases}x_1+x_2=\frac{2\left(m-1\right)}{m}\\x_1x_2=1\end{cases}}\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\frac{4\left(m-1\right)^2}{m^2}-2=3\)
\(\Leftrightarrow m=2\left(-2\pm\sqrt{5}\right)\)
Đối chiếu điều kiện đều thỏa mãn.