Cho hàm số y = m x 3 – x 2 - 2 x + 8 m có đồ thị ( C m ) . Tìm tất cả giá trị tham số m để đồ thị ( C m ) cắt trục hoành tại ba điểm phân biệt
A. m ∈ - 1 6 ; 1 2
B. m ∈ - 1 6 ; 1 2
C. m ∈ - 1 6 ; 1 2 \ 0
D. m ∈ - ∞ ; 1 2 \ 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4

Đáp án B.
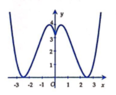
Hàm số y = f x + m là một hàm số chẵn nên đồ thị đối xứng qua trục Oy. Mặt khác y = f x + m = f x + m ∀ x ≥ 0 . Ta có phép biến đổi từ đồ thị hàm số y = f x thành đồ thị hàm số y = f x + m :
* Nếu m > 0:
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang trái m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
* Nếu m=0 :
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang phải m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
Quan sát ta thấy đồ thị hàm số y = f x có 2 điểm cực trị.
Để đồ thị hàm số y = x + m có 5 điểm cực trị thì nhánh bên phải Oy của đồ thị hàm số y = x + m phải có 2 điểm cực trị => Điểm cực trị của đồ thị hàm số y = f x phải được tịnh tiến sang phải O y ⇒ m < − 1 .

Toi mới làm được câu 2 thoi à :( Mấy câu còn lại để rảnh nghĩ thử coi sao
\(PTHDGD:\dfrac{x+1}{x-1}=2x+m\Leftrightarrow x+1=\left(2x+m\right)\left(x-1\right)\)
\(\Leftrightarrow x+1=2x^2-2x+mx-m\Leftrightarrow2x^2+\left(m-3\right)x-m-1=0\)
De ton tai 2 diem phan biet \(\Leftrightarrow\Delta>0\Leftrightarrow\left(m-3\right)^2+8m+8>0\Leftrightarrow m^2+2m+17>0\Leftrightarrow\left(m+1\right)^2+16>0\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{3-m}{2}\\x_1x_2=\dfrac{-m-1}{2}\end{matrix}\right.\)
Vi 2 tiep tuyen tai 2 diem x1, x2 song song voi nhau
\(\Rightarrow f'\left(x_1\right)=f'\left(x_2\right)\)
\(f'\left(x\right)=\dfrac{x-1-x-1}{\left(x-1\right)^2}=-\dfrac{2}{\left(x-1\right)^2}\)
\(\Rightarrow\dfrac{1}{\left(x_1-1\right)^2}=\dfrac{1}{\left(x_2-1\right)^2}\Leftrightarrow x_1^2-2x_1+1=x_2^2-2x_2+1\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)-2\left(x_1-x_2\right)=0\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=x_2\left(loai\right)\\x_1+x_2=2\end{matrix}\right.\Leftrightarrow\dfrac{3-m}{2}=2\Leftrightarrow m=-1\)

Đáp án B.
Phương trình hoành độ giao điểm của (C) và d : x − 2 x − 1 = − x + m
⇔ x ≠ 1 x − 2 = ( − x + m ) ( x − 1 ) ⇔ x ≠ 1 f ( x ) = x 2 − m x + m − 2 = 0 ( * )
Để (C) và d cắt nhau tại hai điểm phân biệt A, B khi và chỉ khi phương trình (*) có hai nghiệm phân biệt x 1 , x 2 khác 1
⇔ f ( 1 ) = 1 2 − m + m − 2 ≠ 0 Δ = - m 2 − 4 ( m − 2 ) > 0 ⇔ − 1 ≠ 0 m 2 − 4 m + 8 m > 0 ⇔ m ∈ ℝ .
Mặt khác OAB là tam giác nên O ∈ d hay m ≠ 0 .
Gọi A ( x 1 ; − x 1 + m ) và B ( x 2 ; − x 2 + m ) . Suy ra O A = 2 x 1 2 − 2 m x 1 + m 2 O B = 2 x 2 2 − 2 m x 2 + m 2
Do x 1 , x 2 là hai nghiệm của phương trình (*) nên x 1 2 − m x 1 = 2 − m x 2 2 − m x 2 = 2 − m
Khi đó O A = 2 ( 2 − m ) + m 2 = m 2 − 2 m + 4 O B = 2 ( 2 − m ) + m 2 = m 2 − 2 m + 4
Từ giả thiết ta có :
2 m 2 − 2 m + 4 = 1 ⇔ m 2 − 2 m + 4 = 2 ⇔ m ( m − 2 ) = 0 ⇔ m = 0 m = 2
Đối chiếu với điều kiện ta được m=2 thỏa mãn.