Cho hai mặt phẳng (P): 2x+y+z-3=0 và (Q): x-y+3z-2=0. Mệnh đề nào sau đây đúng?
A. (P) song song (Q)
B. (P) cắt (Q)
C. (P) trùng (Q)
D. (P) vuông góc (Q)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Phương pháp: Xét hai mặt phẳng
![]()
![]()
+ 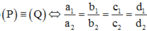 . Khi đó
n
(
P
)
→
/
/
n
Q
→
. Khi đó
n
(
P
)
→
/
/
n
Q
→
+ (P) và (Q) cắt nhau khi và chỉ khi chúng không song song hay trùng nhau
+ (P) ⊥ (Q) <=> n P → ⊥ n Q → ⇔ n P → . n Q → = 0
Cách giải: (P): 2x – y + 3z – 1 = 0; (Q): 4x – 2y + 6z – 1 = 0
Ta có: 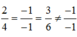
=> (P) và (Q) song song với nhau

Đáp án D
Phương pháp: Xét hai mặt phẳng
![]()
![]()
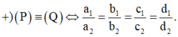
![]()
+) (P) và (Q) cắt nhau khi và chỉ khi chúng không song song hay trùng nhau.
![]()
Cách giải: Ta có: (P): 2x-y+3z-1=0 và (Q): 4x-2y+6z-1=0
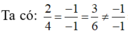
=> (P) và (Q) song song với nhau.

Chọn C.
Đường thẳng d có điểm chung M(1; 1; -1) với cả hai mặt phẳng (P), (Q) và d có vectơ chỉ phương (0; 1; 1) vuông góc với cả hai vectơ pháp tuyến của (P), (Q), do đó d nằm trên cả hai mặt phẳng (P), (Q). Suy ra d = (P) ∩ (Q).