Tìm m để hàm số y = x 3 - 3 x 2 + m x - m 3 có hai điểm cực trị thỏa mãn x 1 , x 2
A. m = - 3 2
B. m = - 3
C. m = 3
D. m = 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$y'=x^2-(m-1)x-m=(x+1)(x-m)$
$y''=2x-(m-1)$
Nếu $x_{ct}=-1$ thì $y''(-1)=-1-m>0\Leftrightarrow m< -1$
$y_{ct}=\frac{1}{2}m+\frac{1}{2}=\frac{1}{3}$
$\Leftrightarrow m=\frac{-1}{3}$ (loại vì $m< -1$)
Nếu $x_{ct}=m$ thì $y''(m)=m+1>0\Leftrightarrow m>-1$
$y_{ct}=\frac{-1}{6}m^3+\frac{1}{2}m^2+\frac{1}{3}=\frac{1}{3}$
$\Leftrightarrow m=0$ (chọn) hoặc $m=-3$ (loại)
Vậy $m=0$

Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

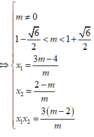

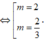

Ta có \(y'=3x^2-3\left(m-2\right)x-3\left(m-1\right)\), với mọi \(x\in R\)
\(y'=0\Leftrightarrow x^2-\left(m-2\right)x-m+1=0\Leftrightarrow x_1=-1;x_2=m-1\)
Chú ý rằng với m > 0 thì \(x_1< x_2\). Khi đó hàm số đạt cực đại tại \(x_1=-1\) và đạt cực tiểu tại \(x_2=m-1\). Do đó :
\(y_{CD}=y\left(-1\right)=\frac{3m}{2};y_{CT}=y\left(m-1\right)=-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\)
Từ giả thiết ta có \(2.\frac{3m}{2}-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\Leftrightarrow6m-6-\left(m+2\right)\left(m-1\right)^2=0\)
\(\Leftrightarrow\left(m-1\right)\left(m^2+m-8\right)=0\Leftrightarrow m=1;m=\frac{-1\pm\sqrt{33}}{2}\)
Đối chiếu yêu cầu m > 0, ta có giá trị cần tìm là \(m=1;m=\frac{-1\pm\sqrt{33}}{2}\)

+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
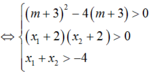
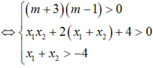
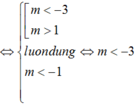
Chọn C

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Đáp án D
y = x 3 − 3 x 2 + m x − m 3 y ' = 3 x 2 − 6 x + m Δ ' = 9 − 3 m > 0 ⇒ m < 3 x 1 2 + x 2 2 = ( 1 + x 2 ) 2 - 2 x 1 x 2 = 4 - 2 . m 3 = 3 ⇔ m = 32