Cho hàm số f x liên tục trên R thỏa mãn điều kiện: f 0 = 2 3 , f 0 > 0 , ∀ x ∈ ℝ và f x . f ' x = 2 x + 1 1 + f 2 x , ∀ x ∈ ℝ . Khi đó giá trị f 1 bằng
A. 15
B. 23
C. 24
D. 26
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


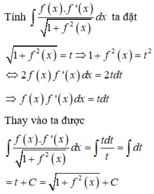
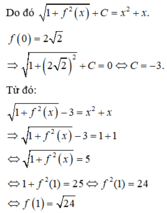

Đáp án C
Ta có f ' x = - e x . f 2 x ⇔ f ' x f 2 x = - e x ⇔ ∫ f ' x f 2 x d x = ∫ - e x d x = ∫ d f x f 2 x d x = - e x + C
⇔ - 1 f x = - e x + C ⇔ f x = 1 e x - C mà f 0 = 1 2 ⇒ 1 1 - C = 1 2 ⇒ C = - 1
Vậy f x = 1 e x + 1 ⇒ f ln 2 = 1 e ln 2 + 1 = 1 2 + 1 = 1 3 .

Đáp án D
Ta có f ' x = - e x . f 2 x ⇔ - f ' x f 2 x = e x ⇔ ∫ - f ' x f 2 x d x = ∫ e x d x ⇔ 1 f x = e x + C
Mà f 0 = 1 2 ⇒ 1 f 0 = e 0 + C ⇔ C + 1 = 2 ⇒ C = 1 → f x = 1 e x + 1
Do đó f ' x = - e x e x + 1 2 ⇒ f ' ln 2 = - 2 9 . Vậy phương trình tiếp tuyến là 2 x + 9 y - 2 ln 2 - 3 = 0 .