Gọi S là tập các giá trị m thỏa mãn hệ sau có nghiệm .Trong tập S có bao nhiêu phần tử là số nguyên?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}x+my=3\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-2\right)y=2\\x=1-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{m-2}\\x=1-\dfrac{4}{m-2}=\dfrac{m-6}{m-2}\end{matrix}\right.\)
a, Ta có x < 0 ; y > 0
\(x< 0\Rightarrow\dfrac{m-6}{m-2}< 0\)
Ta có : m - 2 > m - 6
\(\left\{{}\begin{matrix}m-2>0\\m-6< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>2\\m< 6\end{matrix}\right.\Leftrightarrow2< m< 6\)
\(y>0\Leftrightarrow\dfrac{2}{m-2}>0\Rightarrow m>2\)
Vậy 2 < m < 6
b, \(x-2y=3\Rightarrow\dfrac{m-6}{m-2}-\dfrac{4}{m-2}=3\Leftrightarrow\dfrac{m-10}{m-2}=3\)
\(\Rightarrow m-10=3m-6\Leftrightarrow2m=-4\Leftrightarrow m=-2\)

Chọn B.
Phương pháp:
+ Biến đổi phương trình thứ nhất của hệ để đưa về dạng
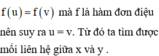
+ Thay vào phương trình thứ hai ta được phương trình ẩn y. Lập luận phương trình này có nghiệm duy nhất
thì hệ ban đầu sẽ có nghiệm duy nhất.

+ Sử dụng bất đẳng thức Cô-si để thử lại m.
Cách giải:



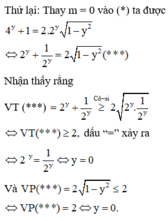
Vậy phương trình (***) có nghiệm duy nhất y = 0.
Kết luận : Với m = 0 thì hệ đã cho có nghiệm duy nhất nên tập S có một phần tử.
Chú ý :
Các em có thể làm bước thử lại như sau :
Thay m = 0 vào (*) ta được
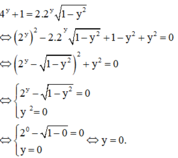



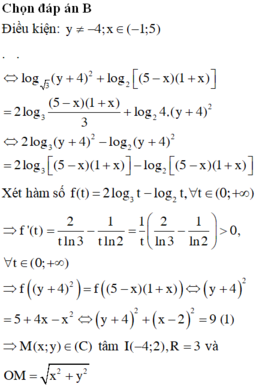
Đáp án A