Hiệu của hai số bình phương là 115. Tìm giá trị nhỏ nhất của bình phương lớn hơn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gợi ý: Hai số lẻ liên tiếp là 2x + 1; 2x + 3 hoặc 2x – 1; 2x + 1. Kết quả: 19; 21.
Tìm hai số tự nhiên lẻ liên tiếp biết bình phương của số lớn lớn hơn bình phương số nhỏ là 80 đơn vị


Đáp án A
Ta có: y ' = 6 x 2 + 6 x − 12 ⇒ y ' = 0 ⇔ x = 1 x = − 2
Suy ra: y − 1 = 15 , y 1 = − 5 , y 2 = 6 ⇒ M = 15 m = − 5 ⇒ M 2 + m 2 = 250.

Đáp án C
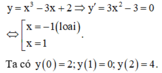
Vậy tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất là 16.

Đáp án A
Gọi số thứ nhất là a; a ∈ N, số thứ hai là b; b ∈ N Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:
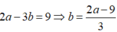
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:
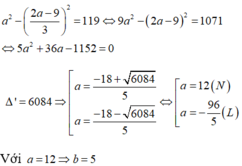
Vậy số lớn hơn là 12.

Đáp án A
Gọi số thứ nhất là a; a ∈ N , số thứ hai là b; b ∈ N
Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:
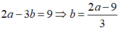
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:
a 2 – b 2 = 119 hay
a 2 − 2 a − 9 3 2 = 119 ⇔ 9 a 2 − 4 a 2 − 36 a + 81 = 119.9 ⇔ 5 a 2 + 36 a − 1152 = 0 T a c ó : Δ ' = 18 2 − 5. − 1152 = 6084 ⇒ Δ ' = 78
Nên phương trình có hai nghiệm
a 1 = − 18 − 78 5 = − 96 5 ( l o ạ i ) ; a 2 = − 18 + 78 5 = 12 ( n h ậ n )
⇒ b = 2.12 − 9 3 = 5

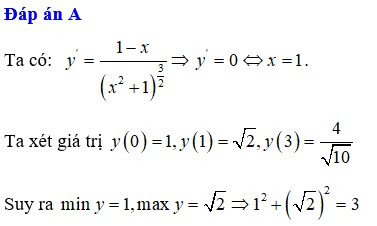


Nếu bình phương lớn là \(a^2\)còn bình phương bé là \(b^2\)thì theo đề bài, ta có: \(a^2-b^2=115\)
\(\Rightarrow a^2=115+b^2\)
Để \(a^2\)nhỏ nhất thì \(b^2\)cũng phải nhỏ nhất, mà \(b^2\ge0\)nên GTNN của \(b^2\)là 0 khi \(b=0\)
Khi đó \(a^2=115+b^2=115+0=115\)
Vậy GTNN của bình phương lớn hơn là 115.