Cho hàm số ![]() liên tục trên khoảng (-3;2),
liên tục trên khoảng (-3;2), 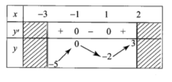
có bảng biến thiên như hình vẽ bên. Khẳng định nào sau
đây là đúng?
A.![]()
B. ![]()
C. ![]()
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Hàm số liên tục tại một điểm

+ Hàm số liên tục trên một khoảng
- Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
- Hàm số y = f(x) được gọi là liên tục trên một đoạn [a; b] nếu nó liên tục tại mọi điểm thuộc khoảng (a;b) và
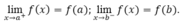
Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.

Ta có ![]()
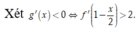
= TH1: ![]() Do đó hàm số nghịch biến trên (-4;-2)
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: ![]() nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số 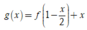 nghịch biến trên (-4;-2)
nghịch biến trên (-4;-2)
Chọn A.

Chọn C
Từ đồ thị hàm số y=f’(x) ta có bảng biến thiên cho hàm số y=f(x) như sau:
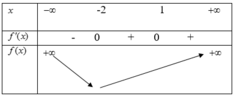
Nhìn vào bảng biến thiên ta thấy ngay trong khoảng (-2;+∞) thì hàm số y=f(x) đồng biến

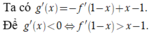
Đặt t = 1 - x, bất phương trình trở thành f'(t) > -t
Kẻ đường thẳng y = -x cắt đồ thị hàm số f'(x) lần lượt tại ba điểm x = -3, x = -1, x = 3 (như hình vẽ)
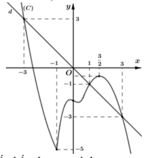
Quan sát đồ thị ta thấy bất phương trình
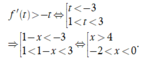
Đối chiếu đáp án ta chọn B.
Đáp án A