Cho hàm số
y
=
4
x
4
-
8
x
2
+
3
. Mệnh đề nào dưới đây đúng? ...
Đọc tiếp
Cho hàm số y = 4 x 4 - 8 x 2 + 3 . Mệnh đề nào dưới đây đúng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
16 tháng 2 2018
Đúng(0)
Những câu hỏi liên quan
CM
1 tháng 1 2018
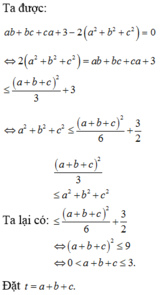
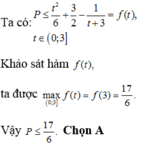
Ta có y ' = − x 2 − 2 x + 8 x 2 + 8 2 ⇒ y ' = 0 ⇔ x = − 4 x = 2
Suy ra, cực đại của hàm số là y 2 = 1 4 .
CM
10 tháng 5 2019
Đáp án C
y = x − sin 2 x + 3 ⇒ y ' = 1 − 2 cos 2 x y ' = 0 ⇔ c os2x= 1 2 ⇔ 2 x = ± π 3 + k 2 π ⇔ x = ± π 6 + k π y ' ' = 4 sin 2 x y ' ' ( − π 6 ) < 0
CM
15 tháng 5 2018
Chọn D
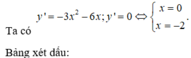
Dựa vào bảng biến thiên, ta thấy hàm số đồng biến trên khoảng (-2;0) và nghịch biến trên các khoảng ( - ∞ ; - 2 ) và ( 0 ; + ∞ )
CM
12 tháng 4 2019
Đáp án D
Ta có: f ' x > 0 ⇔ - 3 < x < 2 f ' x < 0 ⇔ [ x > 2 x < - 3
Suy ra hàm số đồng biến trên khoảng (-3;2), nghịch biến trên các khoảng - ∞ ; - 3 v à 2 ; + ∞ .
CM
12 tháng 12 2017
Đáp án D
Ta có: y ' = 1 x − 2 2 > 0 , ∀ x ≠ 2 ⇒ Hàm số đồng biến trên từng khoảng xác định
CM
4 tháng 9 2019
Đáp án B
Hàm số có tập xác định D = ℝ \ − 2
Ta có y ' = 5 x + 2 2 > 0 , ∀ x ∈ D ⇒ Hàm số đồng biến trên từng khoảng xác định
CM
13 tháng 6 2019
Đáp án D
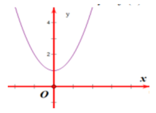
Nhìn vào hình vẽ ta thấy đồ thị nằm hoàn toàn trên trục Ox nên y’>0 với mọi x do đó hàm số y=f(x) đồng biến trên R