Hàm số y = x 4 + b x 2 + c có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây là đúng?
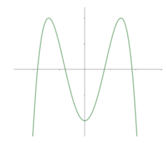
A. a < 0, b > 0, c > 0
B. a < 0, b > 0, c < 0
C. a < 0, b < 0, c > 0
D. a < 0, b < 0, c < 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 6 2019
Chọn đáp án B
Ta thấy hàm số y = a x đồng biến trên ℝ nên a >1; hàm số y = log b x nghịch biến trên 0 ; + ∞ nên 0 <b <1
CM
20 tháng 11 2018
Chọn A
Đồ thị cắt trục tung tại điểm (0;c), từ đồ thị suy ra c < 0
Mặt khác đồ thị hàm số có ba điểm cực trị nên y' = 0 có ba nghiệm phân biệt, hay 
có ba nghiệm phân biệt. Suy ra a,b trái dấu.
Mà a < 0 => b > 0
Vậy chọn A
CM
14 tháng 8 2018
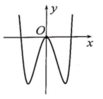
Chọn đáp án D
Ta có: lim x → + ∞ y = + ∞ → Hệ số a > 0 → Loại đáp án B.
Đồ thị hàm số đi qua gốc tọa độ O (0;0) → c = 0 → Loại đáp án A.
Hàm số có 3 điểm cực trị → ab < 0 → b < 0 (Vì a > 0)
→ Loại đáp án C, đáp án D thỏa mãn.
CM
30 tháng 5 2017
Ta vẽ đường thẳng x = 1 cắt các đồ thi hàm số đã cho tại tung độ lần lượt a; b; c
Vậy a < b < c. Chọn B
CM
18 tháng 2 2017
Đáp án B
Ta có hàm số y = b x ; y = c x đồng biến, hàm số y = a x nghịch biến nên a < 1 ; b , c > 1
Thay x = 10 , ta có b 10 > c 10 ⇒ b > c
CM
25 tháng 10 2019
Đáp án A
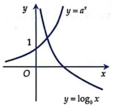
+ Từ đồ thị hàm số y = a x :Với x = 1 ⇒ a > 1
+ Từ đồ thị hàm số y = log b x :Với y = 1 ⇒ x < 1 có log b x = y ⇒ x = b y ⇒ 0 < b < 1
Chọn B
Phương pháp:
Sử dụng cách đo đồ thị hàm số trùng phương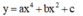
+ Xác định dấu của a dựa vào giới hạn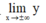
+ Xác định dấu của b dựa vào số cực trị: Hàm số có ba cực trị => a.b < 0, hàm số có 1 cực trị => a.b ≥ 0
+ Xác định dấu của c dựa vào giao điểm của đồ thị với trục tung.
Cách giải:
Từ đồ thị hàm số ta có:
+ Đồ thị hàm số có ba điểm cực trị nên ab < 0 mà a < 0 => b > 0
+ Đồ thị cắt trục tung tại điểm có tung độ âm nên c < 0
Vậy a < 0, b > 0, c > 0