Hàm số
y
=
l
o
g
2
(
4
x
-
2
x
+
m
)
có tập xác định là D+R khi ...
Đọc tiếp
Hàm số y = l o g 2 ( 4 x - 2 x + m ) có tập xác định là D+R khi
K
Khách
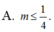
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
CM
29 tháng 9 2018
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Ta thấy hàm số có nghĩa với mọi số thực nên \(D = \mathbb{R}\)
b)
Điều kiện: \(2 - 3x \ge 0 \Leftrightarrow x \le \frac{2}{3}\)
Vậy tập xác định: \(S = \left( { - \infty ;\frac{2}{3}} \right]\)
c) Điều kiện: \(x + 1 \ne 0 \Leftrightarrow x \ne - 1\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
d) Ta thấy hàm số có nghĩa với mọi \(x \in \mathbb{Q}\) và \(x \in \mathbb{R}\backslash \mathbb{Q}\) nên tập xác định: \(D = \mathbb{R}\).
BN
1
Y
12 tháng 3 2023
Hàm số xác định \(\Leftrightarrow\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
Đặt \(f\left(x\right)=\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
\(f\left(x\right)\ge0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\left[-2\left(m-3\right)\right]^2-4\left(m-2\right)\left(m-1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\4\left(m^2-6m+9\right)-4\left(m^2-3m+2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-24m+36-4m^2+12m-8\le0\)
\(\Leftrightarrow-12m+28\le0\)
\(\Leftrightarrow m\le\dfrac{7}{3}\)
\(KL:m\in(2;\dfrac{7}{3}]\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
Hàm có TXĐ là R khi và chỉ khi: \(\left(m-2\right)x^2+\left(m-2\right)x+4\ge0;\forall x\)
- Với \(m=2\) thỏa mãn
- Với \(m\ne2\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\Delta=\left(m-2\right)^2-16\left(m-2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\\left(m-2\right)\left(m-18\right)\le0\end{matrix}\right.\) \(\Rightarrow2< m\le18\)
Kết hợp lại ta được: \(2\le m\le18\)
