Cho hàm số y = 3 x + 2018 2 x - 1 . Khẳng định nào sau đây là khẳng định đúng?
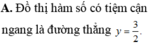

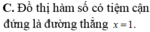
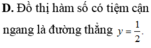
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có y ' = − 2 x − 1 2 < 0 ∀ ≠ 1 ⇒ hàm số nghịch biến trên các khoảng − ∞ ; 1 và 1 ; + ∞

Đáp án D
Phương pháp:
Hàm số dạng y = a x + b c x + d luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.
Cách giải: Tập xác định D = ℝ \ 1
Ta có: y ' = − 1 + 2 x − 1 2 = 1 x − 1 2 > 0 ∀ x ∈ ℝ
Vậy hàm số đồng biến trên các khoảng − ∞ ; 1 và 1 ; + ∞

Chọn B
Hàm số
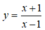
xác định ∀x ≠ 1
Ta có:
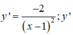
xác định ∀x ≠ 1
Bảng xét dấu đạo hàm
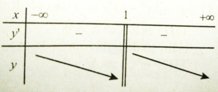
Hàm số nghịch biến trên các khoảng (-∞; 1) và (1; +∞)

Đáp án B
Ta có: lim x → ± ∞ x - 2 - x + 3 = - 1 suy ra TCN: y=-1
lim x → 3 + x - 2 - x + 3 = - ∞ , lim x → 3 - x - 2 - x + 3 = + ∞ suy ra TCĐ: x=3
Chọn A