Cho hình chóp đều S.ABCD có đáy là hình vuông ABCD tâm O cạnh 2a, cạnh bên S A = a 5 . Khoảng cách giữa BD và SC là
A. a 15 5
B. a 30 5
C. a 15 6
D. a 5 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2016
kẻ CE//BD ( E thuộc AD)
=> d( BD;SC)= d( BD; ( SCE))=d( O; ( SCE))
kẻ OK _|_SC
OC_|_ CE
SO_|_CE => CE_|_ ( SOC) => CE_|_OK
do đó OK_|_(SCE)=> d(O;(SCE))=OK
1/OK^2=1/SO^2+1/OC^2
11 tháng 8 2016
câu 2:
BC//AD=> d( BC;SA)=d(BC:(SAD))=d( B;( SAD))=2 d( O; (SAD))
kẻ OH_|_ AD
kẻ OE_|_SH
ta có OH_|_AD; SO_|_AD=> AD_|_(SOH)=> AD_|_ OE
do đó OE_|_( SAD)=> d( O; (SAD))=OE
CM
5 tháng 10 2019
Đáp án D
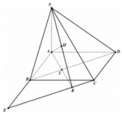
Dựng 
Dựng 
Khi đó Cx cắt AB tại E và AK tại I suy ra BI là đường trung bình của ∆AEK ( Do BD qua trung điểm O của AC)
Ta có: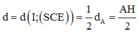 
Do 
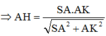
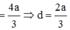
Chọn đáp án B
Phương pháp
+) Dựng đoạn vuông góc chung của BD và SC.
+) Áp dụng hệ thức lượng trong tam giác vuông tính độ dài vuông góc chung.
Cách giải