Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
1
2
+
y
−
2
2
+
z
−
3
2
=
16
và các điểm
A
1
;
0
;
2
,
B
−
1
;
2
;
2
.
Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y − 2 2 + z − 3 2 = 16 và các điểm A 1 ; 0 ; 2 , B − 1 ; 2 ; 2 . Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của mặt phẳng (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng a x + b y + c z + 3 = 0. Tính tổng T = a + b + c
A. 3
B. -3
C. 0
D. -2
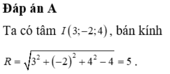
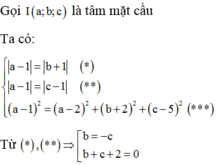
Đáp án B
Gọi J là hình chiếu vuông góc của I lên AB
A B → ( − 2 ; 2 ; 0 ) ⇒ A B : x = 1 − t y = t z = 2 J ∈ A B ⇒ J ( 1 − t ; t ; 2 ) ⇒ IJ → ( − t ; t − 2 ; − 1 ) IJ → . A B → = 0 ⇔ 2 t + 2 t − 4 = 0 ⇔ t = 1 ⇒ J ( 0 ; 1 ; 2 )
Thiết diện của (P) với (S) có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ I đến (P) lớn nhất khi và chỉ khi d ( I ; ( P ) ) = d ( I ; A B ) = IJ
Vậy (P) là mặt phẳng đi qua J và có VTPT IJ →
⇒ ( P ) : x + ( y − 1 ) + ( z − 2 ) = 0 ⇔ − x − y − z + 3 = 0 ⇒ T = − 3