giải hộ mìn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
6 tháng 5 2021
Câu 20:
\(S=\frac{2}{1.4.7}+\frac{2}{4.7.10}+...+\frac{2}{34.37.40}\)
\(3S=\frac{6}{1.4.7}+\frac{6}{4.7.10}+....+\frac{6}{34.37.40}=\frac{7-1}{1.4.7}+\frac{10-4}{4.7.10}+...+\frac{40-34}{34.37.40}\)
\(=\frac{1}{1.4}-\frac{1}{4.7}+\frac{1}{4.7}-\frac{1}{7.10}+...+\frac{1}{34.37}-\frac{1}{37.40}\)
\(=\frac{1}{1.4}-\frac{1}{37.40}=\frac{369}{1480}\)
$S=\frac{123}{1480}$
20 tháng 2 2023
Ta có : \(\dfrac{56}{24}>1\) do tử > mẫu
\(\dfrac{55}{33}>1\) do tử > mẫu
\(\dfrac{126}{168}< 1\) tử bé hơn mẫu nên ta chỉ xét hai phân số : \(\dfrac{56}{24};\dfrac{55}{33}\)
Ta lại có : \(\dfrac{56}{24}=\dfrac{7}{3}\)
\(\dfrac{55}{33}=\dfrac{5}{3}\)
do 7>5 suy ra : \(\dfrac{56}{24}>\dfrac{55}{33}\)
\(\Rightarrow\dfrac{126}{168}< \dfrac{55}{33}< \dfrac{56}{24}\)
20 tháng 2 2023
\(\dfrac{56}{24}=\dfrac{7}{3}\) ( cùng chia cả tử và mẫu cho 8 )
\(\dfrac{126}{168}=\dfrac{3}{4}\)( cùng chia cả tử và mẫu cho 42 )
\(\dfrac{55}{33}=\dfrac{5}{3}\) ( cùng chia cả tử và mẫu cho 11 )
SS
22 tháng 6 2019
\(B=\left(1-\frac{2}{5}\right)\left(1-\frac{2}{7}\right)\left(1-\frac{2}{9}\right)....\left(1-\frac{2}{99}\right)\)
\(B=\frac{3}{5}\cdot\frac{5}{7}\cdot\frac{7}{9}\cdot...\cdot\frac{97}{99}\)
\(B=\frac{3\cdot5\cdot7\cdot...\cdot97}{5\cdot7\cdot9\cdot...\cdot99}=\frac{3}{99}=\frac{1}{33}\)
Vậy B = \(\frac{1}{33}\)
22 tháng 6 2019
\(\left[1-\frac{2}{5}\right]\left[1-\frac{2}{7}\right]\left[1-\frac{2}{9}\right]...\left[1-\frac{2}{99}\right]\)
\(=\frac{3}{5}\cdot\frac{5}{7}\cdot\frac{7}{9}\cdot...\cdot\frac{97}{99}\)
\(=\frac{3\cdot5\cdot7\cdot...\cdot97}{5\cdot7\cdot9\cdot...\cdot99}=\frac{3}{99}=\frac{1}{33}\)
HN
2
3 tháng 4 2018
\(x-\frac{4}{9}=\frac{8}{13}+\frac{6}{5}\)
\(x-\frac{4}{9}=\frac{118}{65}\)
\(x=\frac{118}{65}+\frac{4}{9}=\frac{1322}{585}\)
SG
3 tháng 4 2018
\(x-\frac{4}{9}=\frac{8}{13}+\frac{6}{5}\)
\(x-\frac{4}{9}=\frac{40}{65}+\frac{78}{65}\)
\(x-\frac{4}{9}=\frac{118}{65}\)
\(x=\frac{118}{65}+\frac{4}{9}\)
\(x=?\)
Tự tính nha!
TD
3 tháng 8 2021
( hot/ off/ Take/ it's/ hat/ your/ . )
=> Take off your hat it's hot.
Hc tốt
LM
0
NH
1
HC
24 tháng 9 2019
(1-4sin^2 x)sin3x=1/2
1+sin(x/2)sinx-cos(x/2)sin^2 x=2cos^2 (pi/4-x/2)
(sin^3 x.sin3x+cos^3 x.cos3x)/tan(x-pi/6)tan(x+pi/3)=-1/8
2cos^2 (pi/4-3x)-4cos4x-15sin2x=21
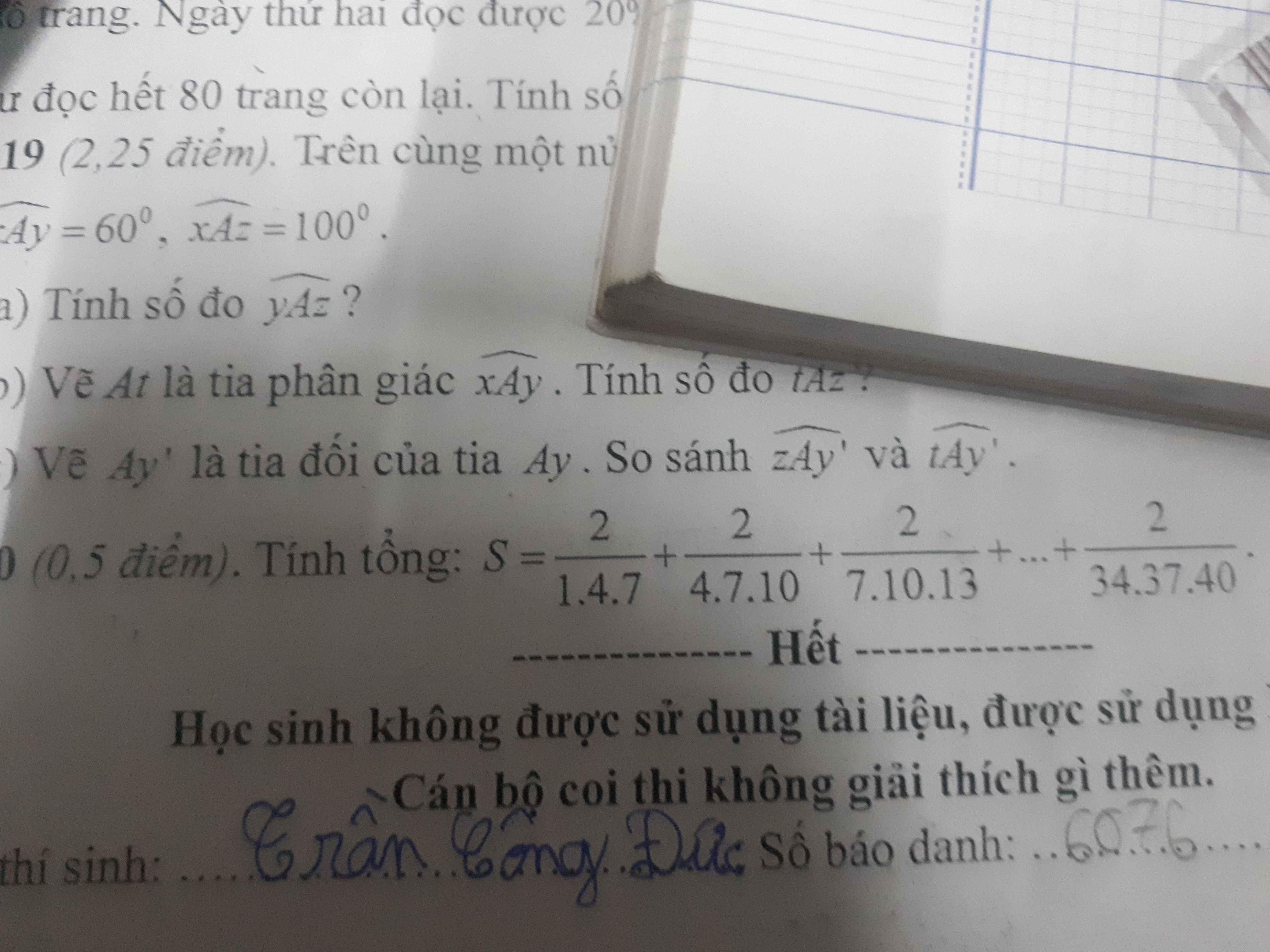
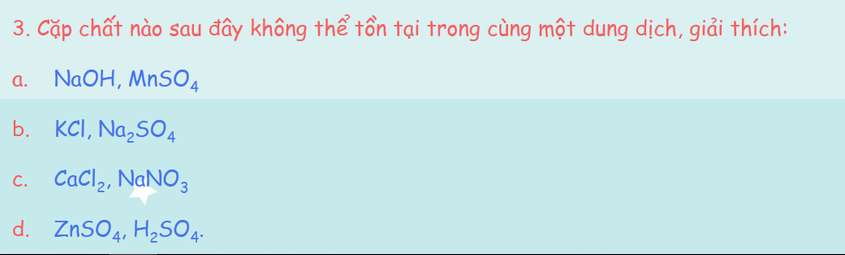bạn nào hộ mìn với ỤnU