Cho hàm số bậc ba y = f x có đồ thị (C) như hình vẽ, đường thẳng d có phương trình
y = x -1. Biết phương trình f x = 0 có ba nghiệm x 1 < x 2 < x 3 . Giá trị của x 1 x 3 bằng
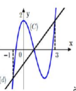
A. - 2
B. - 5 2
C. 1
D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D
Từ đồ thị f ’(x) ta lập được BBT của f(x)
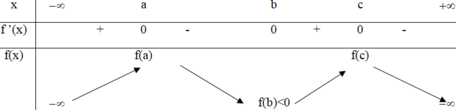
=> Có 4 nghiệm là nhiều nhất

Đáp án C
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).
Chọn A.
Phương pháp:
Gọi hàm số cần tìm là y = f x = a x 3 + b x 2 + c x + d
Xác định các điểm thuộc đồ thị hàm số rồi thay tọa độ vào hàm số để được hệ bốn ẩn
Giải hệ ta tìm được a;b;c;d . Từ đó tìm nghiệm phương trình f(x)=0 .