Cho biết 9^x -12^2 =0, tính giá trị biểu thức P = 1 3 - x - 1 - 8 . 9 x - 1 2 + 19 .
A. 15
B. 31
C. 23
D. 22
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 11 2017
Đúng(0)
Những câu hỏi liên quan
H
8 tháng 2 2023
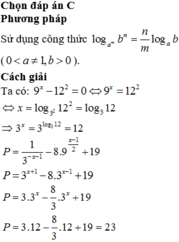
`5`
`a, -7/21 +(1+1/3)`
`=-7/21 + ( 3/3 + 1/3)`
`=-7/21+ 4/3`
`=-7/21+ 28/21`
`= 21/21`
`=1`
`b, 2/15 + ( 5/9 + (-6)/9)`
`= 2/15 + (-1/9)`
`= 1/45`
`c, (9-1/5+3/12) +(-3/4)`
`= ( 45/5-1/5 + 3/12)+(-3/4)`
`= ( 44/5 + 3/12)+(-3/4)`
`= 9,05 +(-0,75)`
`=8,3`
`6`
`x+7/8 =13/12`
`=>x= 13/12 -7/8`
`=>x=5/24`
`-------`
`-(-6)/12 -x=9/48`
`=> 6/12 -x=9/48`
`=>x= 6/12-9/48`
`=>x=5/16`
`---------`
`x+4/6 =5/25 -(-7)/15`
`=>x+4/6 =1/5 + 7/15`
`=> x+ 4/6=10/15`
`=>x=10/15 -4/6`
`=>x=0`
`----------`
`x+4/5 = 6/20 -(-7)/3`
`=>x+4/5 = 6/20 +7/3`
`=>x+4/5 = 79/30`
`=>x=79/30 -4/5`
`=>x= 79/30-24/30`
`=>x= 55/30`
`=>x= 11/6`
VN
8 tháng 2 2023
\(5)\)
\(A=\dfrac{-7}{21}+\left(1+\dfrac{1}{3}\right)\)
\(A=\dfrac{-7}{21}+\dfrac{4}{3}\)
\(A=\dfrac{-7}{21}+\dfrac{28}{21}\)
\(A=1\)
\(--------------\)
\(B=\dfrac{2}{15}+\left(\dfrac{5}{9}+\dfrac{-6}{9}\right)\)
\(B=\dfrac{2}{15}+\dfrac{-1}{9}\)
\(B=\dfrac{18}{135}+\dfrac{-15}{135}\)
\(B=\dfrac{1}{45}\)
\(------------\)
\(C=9-\dfrac{1}{5}+\dfrac{3}{12}+\dfrac{-3}{4}\)
\(C=\dfrac{44}{5}+\dfrac{3}{12}+\dfrac{-3}{4}\)
\(C=\dfrac{528}{60}+\dfrac{15}{60}+\dfrac{-3}{4}\)
\(C=\dfrac{181}{20}+\dfrac{-3}{4}\)
\(C=\dfrac{181}{20}+\dfrac{-15}{20}\)
\(C=\dfrac{83}{10}\)
\(6)\)
\(a)\) \(x+\dfrac{7}{8}=\dfrac{13}{12}\)
\(x=\dfrac{13}{12}-\dfrac{7}{8}\)
\(x=\dfrac{104}{96}-\dfrac{84}{96}\)
\(x=\dfrac{5}{24}\)
\(b)\) \(\dfrac{-6}{12}-x=\dfrac{9}{48}\)
\(\dfrac{-1}{2}-x=\dfrac{3}{16}\)
\(x=\dfrac{-1}{2}-\dfrac{3}{16}\)
\(x=\dfrac{-8}{16}-\dfrac{3}{16}\)
\(x=\dfrac{-11}{16}\)
\(c)\) \(x+\dfrac{4}{6}=\dfrac{5}{25}-\left(-\dfrac{7}{15}\right)\)
\(x+\dfrac{4}{6}=\dfrac{5}{25}+\dfrac{7}{15}\)
\(x+\dfrac{4}{6}=\dfrac{75}{375}+\dfrac{105}{375}\)
\(x+\dfrac{4}{6}=\dfrac{12}{25}\)
\(x=\dfrac{12}{25}-\dfrac{4}{6}\)
\(x=\dfrac{72}{150}-\dfrac{100}{150}\)
\(x=\dfrac{-14}{75}\)
\(d)\) \(x+\dfrac{4}{5}=\dfrac{6}{20}-\left(-\dfrac{7}{3}\right)\)
\(x+\dfrac{4}{5}=\dfrac{6}{20}+\dfrac{7}{3}\)
\(x+\dfrac{4}{5}=\dfrac{18}{60}+\dfrac{140}{60}\)
\(x+\dfrac{4}{5}=\dfrac{79}{30}\)
\(x=\dfrac{79}{30}-\dfrac{4}{5}\)
\(x=\dfrac{79}{30}-\dfrac{24}{30}\)
\(x=\dfrac{11}{6}\)
A
1 tháng 3 2018
Bài 1) Chứng minh rằng các biểu thức sau luôn có giá trị âm với mọi giá trị của biến:
a) 9x^2+12x-15
=-(9x^2-12x+4+11)
=-[(3x-2)^2+11]
=-(3x-2)^2 - 11.
Vì (3x-2)^2 không âm với mọi x suy ra -(3x-2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x
Do đó -[(3*x)-2]^2-11 < 0 với mọi giá trị của x.
Hay -9*x^2 + 12*x -15 < 0 với mọi giá trị của x.
b) -5 – (x-1)*(x+2)
= -5-(x^2+x-2)
=-5- (x^2+2x.1/2 +1/4 - 1/4-2)
=-5-[(x-1/2)^2 -9/4]
=-5-(x-1/2)^2 +9/4
=-11/4 - (x-1/2)^2
Vì (x-1/2)^2 không âm với mọi x suy ra -(x-1/2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x
Do đó -11/4 - (x-1/2)^2 < 0 với mọi giá trị của x.
Hay -5 – (x-1)*(x+2) < 0 với mọi giá trị của x.
Bài 2)
a) x^4+x^2+2
Vì x^4 +x^2 lớn hơn hoặc bằng 0 vơi mọi x
suy ra x^4+x^2+2 >=2
Hay x^4+x^2+2 luôn dương với mọi x.
b) (x+3)*(x-11) + 2003
= x^2-8x-33 +2003
=x^2-8x+16b + 1954
=(x-4)^2 + 1954 >=1954
Vậy biểu thức luôn có giá trị dương với mọi giá trị của biến
1) Cho biểu thức A =
7 tháng 9 2021
Bài 5:
a: Thay \(x=4+2\sqrt{3}\) vào E, ta được:
\(E=\dfrac{\sqrt{3}+1-1}{\sqrt{3}+1-3}=\dfrac{\sqrt{3}}{\sqrt{3}-2}=-3-2\sqrt{3}\)
b: Để E<1 thì E-1<0
\(\Leftrightarrow\dfrac{\sqrt{x}-1-\sqrt{x}+3}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
hay x<9
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne1\end{matrix}\right.\)
c: Để E nguyên thì \(4⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{-2;1;2;4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;5;7\right\}\)
hay \(x\in\left\{16;25;49\right\}\)
NT
7 tháng 9 2021
Câu 2:
a) Ta có \(x=4-2\sqrt{3}\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}-2\right)^2}=\sqrt{3}-2\)
Thay \(x=\sqrt{3}-1\) vào \(B\), ta được
\(B=\dfrac{\sqrt{3}-1-2}{\sqrt{3}-1+1}=\dfrac{\sqrt{3}-3}{\sqrt{3}}=1-\sqrt{3}\)
b) Để \(B\) âm thì \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< 0\) mà \(\sqrt{x}+1\ge1>0\forall x\) \(\Rightarrow\sqrt{x}-2< 0\Rightarrow\sqrt{x}< 2\Rightarrow x< 4\)
c) Ta có \(B=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=1-\dfrac{3}{\sqrt{x}+1}\)
Với mọi \(x\ge0\) thì \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+1\ge1\Rightarrow\dfrac{3}{\sqrt{x}+1}\le3\Rightarrow B=1-\dfrac{3}{\sqrt{x}+1}\ge-2\)
Dấu "=" xảy ra khi \(\sqrt{x}+1=1\Leftrightarrow x=0\)
Vậy \(B_{min}=-2\) khi \(x=0\)