Tích tất cả các nghiệm của phương trình log 3 2 x - 2 log 3 x - 7 = 0 là
A. 9
B. -7
C. 1
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
\(a,0,1^{2-x}>0,1^{4+2x}\\ \Leftrightarrow2-x>2x+4\\ \Leftrightarrow3x< -2\\ \Leftrightarrow x< -\dfrac{2}{3}\)
\(b,2\cdot5^{2x+1}\le3\\ \Leftrightarrow5^{2x+1}\le\dfrac{3}{2}\\ \Leftrightarrow2x+1\le log_5\left(\dfrac{3}{2}\right)\\ \Leftrightarrow2x\le log_5\left(\dfrac{3}{2}\right)-1\\ \Leftrightarrow x\le\dfrac{1}{2}log_5\left(\dfrac{3}{2}\right)-\dfrac{1}{2}\\ \Leftrightarrow x\le log_5\left(\dfrac{\sqrt{30}}{10}\right)\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
c, ĐK: \(x>-7\)
\(log_3\left(x+7\right)\ge-1\\ \Leftrightarrow x+7\ge\dfrac{1}{3}\\ \Leftrightarrow x\ge-\dfrac{20}{3}\)
Kết hợp với ĐKXĐ, ta có:\(x\ge-\dfrac{20}{3}\)
d, ĐK: \(x>\dfrac{1}{2}\)
\(log_{0,5}\left(x+7\right)\ge log_{0,5}\left(2x-1\right)\\ \Leftrightarrow x+7\le2x-1\\ \Leftrightarrow x\ge8\)
Kết hợp với ĐKXĐ, ta được: \(x\ge8\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
\(a,3^x>\dfrac{1}{243}\\ \Leftrightarrow3^x>3^{-5}\\ \Leftrightarrow x>-5\\ b,\left(\dfrac{2}{3}\right)^{3x-7}\le\dfrac{3}{2}\\ \Leftrightarrow3x-7\le1\\ \Leftrightarrow3x\le8\\ \Leftrightarrow x\le\dfrac{8}{3}\\ c,4^{x+3}\ge32^x\\ \Leftrightarrow2^{2x+6}\ge2^{5x}\\ \Leftrightarrow2x+6\ge5x\\ \Leftrightarrow3x\le6\\ \Leftrightarrow x\le2\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
d, Điều kiện: x > 1
\(log\left(x-1\right)< 0\\ \Leftrightarrow x-1< 1\\ \Leftrightarrow1< x< 2\)
e, Điều kiện: \(x>\dfrac{1}{2}\)
\(log_{\dfrac{1}{5}}\left(2x-1\right)\ge log_{\dfrac{1}{5}}\left(x+3\right)\\ \Leftrightarrow2x-1\ge x+3\\ \Leftrightarrow x\ge4\)
f, Điều kiện: x > 4
\(ln\left(x+3\right)\ge ln\left(2x-8\right)\\ \Leftrightarrow x+3\ge2x-8\\\Leftrightarrow4< x\le11\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) \({3^{{x^2} - 4x + 5}} = 9 \Leftrightarrow {x^2} - 4x + 5 = 2 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left( {x - 3} \right)\left( {x - 1} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Vậy phương trình có nghiệm là \(x \in \left\{ {1;3} \right\}\)
b) \(0,{5^{2x - 4}} = 4 \Leftrightarrow 2x - 4 = {\log _{0,5}}4 \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\)
Vậy phương trình có nghiệm là x = 1
c) \({\log _3}(2x - 1) = 3\) ĐK: \(2x - 1 > 0 \Leftrightarrow x > \frac{1}{2}\)
\( \Leftrightarrow 2x - 1 = 27 \Leftrightarrow x = 14\) (TMĐK)
Vậy phương trình có nghiệm là x = 14
d) \(\log x + \log (x - 3) = 1\) ĐK: \(x - 3 > 0 \Leftrightarrow x > 3\)
\(\begin{array}{l} \Leftrightarrow \log \left( {x.\left( {x - 3} \right)} \right) = 1\\ \Leftrightarrow {x^2} - 3x = 10\\ \Leftrightarrow {x^2} - 3x - 10 = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2 (loại) \,\,\,\\x = 5 (TMĐK) \,\,\,\,\,\,\,\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm x = 5
HQ
Hà Quang Minh
Giáo viên
26 tháng 8 2023
\(a,\left(\dfrac{1}{4}\right)^{x-2}=\sqrt{8}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{2x-4}=\left(\dfrac{1}{2}\right)^{-\dfrac{3}{2}}\\ \Leftrightarrow2x-4=-\dfrac{3}{2}\\ \Leftrightarrow2x=\dfrac{5}{2}\\ \Leftrightarrow x=\dfrac{5}{4}\)
\(b,9^{2x-1}=81\cdot27^x\\ \Leftrightarrow3^{4x-2}=3^{4+3x}\\ \Leftrightarrow4x-2=4+3x\\ \Leftrightarrow x=6\)
HQ
Hà Quang Minh
Giáo viên
26 tháng 8 2023
c, ĐK: \(x-2>0\Rightarrow x>2\)
\(2log_5\left(x-2\right)=log_59\\
\Leftrightarrow log_5\left(x-2\right)^2=log_59\\
\Leftrightarrow\left(x-2\right)^2=3^2\\
\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm là x = 5.
d, ĐK: \(x-1>0\Leftrightarrow x>1\)
\(log_2\left(3x+1\right)=2-log_2\left(x-1\right)\\ \Leftrightarrow log_2\left(3x+1\right)\left(x-1\right)=2\\ \Leftrightarrow3x^2-2x-1=4\\ \Leftrightarrow3x^2-2x-5=0\\ \Leftrightarrow\left(3x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm \(x=\dfrac{5}{3}\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) \({\log _{\frac{1}{7}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\) (ĐK: \(x + 1 > 0;2 - x > 0 \Leftrightarrow - 1 < x < 2\))
\(\begin{array}{l} \Leftrightarrow {\log _{{7^{ - 1}}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow - {\log _7}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow {\log _7}{\left( {x + 1} \right)^{ - 1}} > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow {\left( {x + 1} \right)^{ - 1}} > 2 - x\\ \Leftrightarrow \frac{1}{{x + 1}} - 2 + x > 0\\ \Leftrightarrow \frac{{1 + \left( {x - 2} \right)\left( {x + 1} \right)}}{{x + 1}} > 0\\ \Leftrightarrow \frac{{1 + {x^2} - x - 2}}{{x + 1}} > 0 \Leftrightarrow \frac{{{x^2} - x - 1}}{{x + 1}} > 0\end{array}\)
Mà – 1 < x < 2 nên x + 1 > 0
\( \Leftrightarrow {x^2} - x - 1 > 0 \Leftrightarrow \left[ \begin{array}{l}x < \frac{{1 - \sqrt 5 }}{2}\\x > \frac{{1 + \sqrt 5 }}{2}\end{array} \right.\)
KHĐK ta có \(\left[ \begin{array}{l} - 1 < x < \frac{{1 - \sqrt 5 }}{2}\\\frac{{1 + \sqrt 5 }}{2} < x < 2\end{array} \right.\)
b) \(2\log \left( {2x + 1} \right) > 3\) (ĐK: \(2x + 1 > 0 \Leftrightarrow x > \frac{{ - 1}}{2}\))
\(\begin{array}{l} \Leftrightarrow \log \left( {2x + 1} \right) > \frac{3}{2}\\ \Leftrightarrow 2x + 1 > {10^{\frac{3}{2}}} = 10\sqrt {10} \\ \Leftrightarrow x > \frac{{10\sqrt {10} - 1}}{2}\end{array}\)
KHĐK ta có \(x > \frac{{10\sqrt {10} - 1}}{2}\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
\(a,\left(0,3\right)^{x-3}=1\\ \Leftrightarrow x-3=0\\ \Leftrightarrow x=3\\ b,5^{3x-2}=25\\ \Leftrightarrow3x-2=2\\ \Leftrightarrow3x=4\\ \Leftrightarrow x=\dfrac{4}{3}\\ c,9^{x-2}=243^{x+1}\\ \Leftrightarrow3^{2x-4}=3^{5x+5}\\ \Leftrightarrow2x-4=5x+5\\ \Leftrightarrow3x=-9\\ \Leftrightarrow x=-3\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
d, Điều kiện: \(x>-1;x\ne0\)
\(log_{\dfrac{1}{x}}\left(x+1\right)=-3\\ \Leftrightarrow x+1=x^3\\ x\simeq1,325\left(tm\right)\)
e, Điều kiện: \(x>\dfrac{5}{3}\)
\(log_5\left(3x-5\right)=log_5\left(2x+1\right)\\ \Leftrightarrow3x-5=2x+1\\ \Leftrightarrow x=6\left(tm\right)\)
f, Điều kiện: \(x>\dfrac{1}{2}\)
\(log_{\dfrac{1}{7}}\left(x+9\right)=log_{\dfrac{1}{7}}\left(2x-1\right)\\ \Leftrightarrow x+9=2x-1\\ \Leftrightarrow x=10\left(tm\right)\)
20 tháng 1
a: ĐKXĐ: \(4x-3>0\)
=>x>3/4
\(log_5\left(4x-3\right)=2\)
=>\(log_5\left(4x-3\right)=log_525\)
=>4x-3=25
=>4x=28
=>x=7(nhận)
b: ĐKXĐ: \(x\ne0\)
\(log_2x^2=2\)
=>\(log_2x^2=log_24\)
=>\(x^2=4\)
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{-\dfrac{1}{2};\dfrac{3}{2}\right\}\)
\(\log_52x+1=\log_5-2x+3\)
=>2x+1=-2x+3
=>4x=2
=>\(x=\dfrac{1}{2}\left(nhận\right)\)
d: ĐKXD: \(x\notin\left\{3\right\}\)
\(ln\left(x^2-6x+7\right)=ln\left(x-3\right)\)
=>\(x^2-6x+7=x-3\)
=>\(x^2-7x+10=0\)
=>(x-2)(x-5)=0
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=5\left(nhận\right)\end{matrix}\right.\)
e: ĐKXĐ: \(x\notin\left\{\dfrac{1}{5};2\right\}\)
\(log\left(5x-1\right)=log\left(4-2x\right)\)
=>5x-1=4-2x
=>7x=5
=>\(x=\dfrac{5}{7}\left(nhận\right)\)
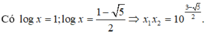
Chọn A
Phương pháp
- Đặt log 3 x = t đưa về phương trình bậc hai ẩn t.
- Tìm mối quan hệ giữa các nghiệm x của phương trình đầu với các nghiệm t tương ứng của phương trình sau và tính toán