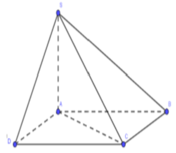
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = a , B C = a 3 , cạnh S A = 2 a , S A ⊥ A B C D . Gọi α là góc giữa đường thẳng SC với mặt phẳng (ABCD). Giá trị tan α bằng
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?

Chắc đề là \(SM=a\sqrt{3}\) vì không có điểm H nào trong dữ liệu
\(BC=AD=\sqrt{BD^2-AB^2}=a\sqrt{2}\)
a.
Qua M kẻ đường thẳng song song BC cắt CD tại E
\(\Rightarrow CD\perp ME\Rightarrow CD\perp\left(SME\right)\)
\(\Rightarrow\widehat{SEM}\) là góc giữa (SCD) và (ABCD)
Áp dụng định lý talet trong tam giác BCD:
\(\dfrac{EM}{BC}=\dfrac{DM}{BD}=\dfrac{3}{4}\Rightarrow EM=\dfrac{3}{4}BC=\dfrac{3a\sqrt{2}}{4}\)
\(\Rightarrow tan\widehat{SEM}=\dfrac{SM}{EM}=\dfrac{2\sqrt{6}}{3}\)
\(\Rightarrow\widehat{SEM}\approx58^031'\)
b.
\(BC||AD\Rightarrow BC||\left(SAD\right)\)
\(\Rightarrow d\left(BC;AD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Lại có: BM cắt (SAD) tại D, mà \(BD=\dfrac{4}{3}MD\)
\(\Rightarrow d\left(B;\left(SAD\right)\right)=\dfrac{4}{3}d\left(M;\left(SAD\right)\right)\)
Trong mp (ABCD), từ M kẻ \(MH\perp AD\)
Trong mp (SMH), từ M kẻ \(MK\perp SH\)
\(\Rightarrow MK\perp\left(SAD\right)\Rightarrow MK=d\left(M;\left(SAD\right)\right)\)
Talet cho tam giác ABD:
\(\dfrac{MH}{AB}=\dfrac{MD}{BD}=\dfrac{3}{4}\Rightarrow MH=\dfrac{3}{4}AB=\dfrac{3a}{4}\)
Hệ thức lượng trong tam giác vuông SMH:
\(MK=\dfrac{SM.MH}{\sqrt{SM^2+MH^2}}=\dfrac{3a\sqrt{19}}{19}\)
\(\Rightarrow d\left(SD;BC\right)=\dfrac{4}{3}MK=\dfrac{4\sqrt{19}}{19}\)

Chọn A
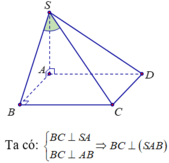
=> SB là hình chiếu của SC lên mặt phẳng (SAB).
![]() .
.
Xét tam giác SBC vuông tại B có ![]()
Xét tam giác SAB vuông tại A có:
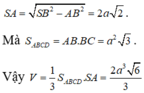

THAM KHẢO:

CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)

Chọn đáp án D
Gọi O là tâm của hình chữ nhật ABCD và I là trung điểm của SC. Khi đó OI ⊥ (ABCD)
⇒ IA = IB = IC = ID với ∆ S A C vuông tại A, IA = IS = IC. Do đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD suy ra IA = a 2 ⇒ SC = 2a 2 . Mặt khác AC là hình chiếu của SC trên mặt phẳng (ABCD).
![]()
Suy ra ∆ S A C vuông cân
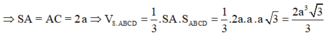

Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ