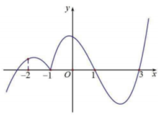
Cho hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu số nguyên m để bất phương trình m x + m 2 5 - x 2 + 2 m + 1 f ( x ) ≥ 0 nghiệm đúng với mọi m ∈ - 2 ; 2 ?
A. 1
B. 3
C. 0
D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
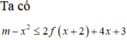
![]()
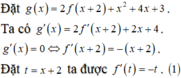
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
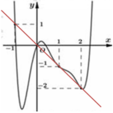
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có



Đặt g ( x ) = m x + m 2 5 - x 2 + 2 m + 1 f ( x ) thì g(x) là hàm số liên tục trên [-2;2]
Từ đồ thị =f(x) ta thấy có nghiệm đối dấu là x=1
Do đó để bất phương trình m x + m 2 5 - x 2 + 2 m + 1 f ( x ) ≥ 0 nghiệm đúng với mọi x ∈ - 2 ; 2 thì điều kiện cần là x=1 phải là nghiệm của h ( x ) = m x + m 2 5 - x 2 + 2 m + 1
h ( 1 ) = m + 2 m 2 + 2 m + 1 ⇔ [ m = - 1 m = - 0 , 5
Do bài cần m nguyên nên ta thử lại với m=-1
h ( x ) = 5 - x 2 - x - 1 ≥ 0 , ∀ x ∈ - 2 ; 1
và h ( x ) = 5 - x 2 - x - 1 ≤ 0 , ∀ x ∈ - 2 ; 1
Dựa theo dấu y=f(x) trên đồ thị ta suy ra
g ( x ) = m x + m 2 5 - x 2 + 2 m + 1 f ( x ) ≥ 0 , ∀ x ∈ - 2 ; 2
Vậy m=-1 thỏa mãn điều kiện bài ra.
Chọn đáp án A.