Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Để hàm số có ba điểm cực trị khi và chỉ khi ab< 0 hay 1.( -2m) <0
Suy ra m> 0
Khi đó
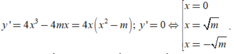
Suy ra tọa độ các điểm cực trị của đồ thị hàm số là:
A 0 ; 2 , B m ; - m 2 + 2 , C - m ; - m 2 + 2
Ycbt O A . O B . O C = 12 ⇔ 2 m + - m 2 + 2 2 = 12
Giải ra ta được m=2; có một giá trị nguyên.
Chọn B.
Hàm số y = f x với f(x) là hàm đa thức bậc 3 có 5 điểm cực trị khi và chỉ khi hàm số f(x) có hai cực trị và đồ thị của hàm số cắt trục hoành tại 3 điểm phân biệt.
Mặt khác, f(x) là hàm số bậc 3 nên khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì hàm số đồng thời cũng có hai cực trị. Do đó ta chỉ cần tìm điều kiện để phương trình f(x) = 0 có 3 nghiệm phân biệt.
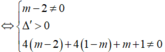
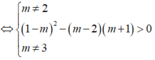
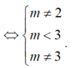
Chọn D
Đơn giản là bạn vẽ cái hàm bậc 4 đó ra và cho -m và -m-10 cắt thôi. Vì -m-10<-m nên -m-10 sẽ nằm ở dưới, còn -m nằm trên. Nên -m sẽ cắt 2 điểm và -m-10 cắt 4 điểm cho ta 6 điểm. Ngoài ra k còn trường hợp nào khác mà -m và -m-10 cắt thỏa mãn
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Ta có : y’ = 4x3-4( m+ 1) x= 4x( x2- (m+ 1) ).
Hàm số có điểm cực trị khi và chỉ khi y’ = 0 có nghiệm phân biệt hay m+1> 0 suy ra m> - 1. (*)
Khi đó, ta có:
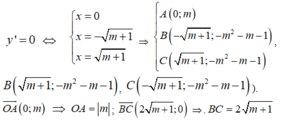
Do đó O A = B C ⇔ m = 2 m + 1 ⇔ m 2 - 4 m - 4 = 0 ( ∆ ' = 8 ) ⇔ m = 2 ± 2 2 (thỏa mãn (*)).
Vậy m = 2 ± 2 2 .
Chọn A.
Đáp án C