Bài 5,6 ạ 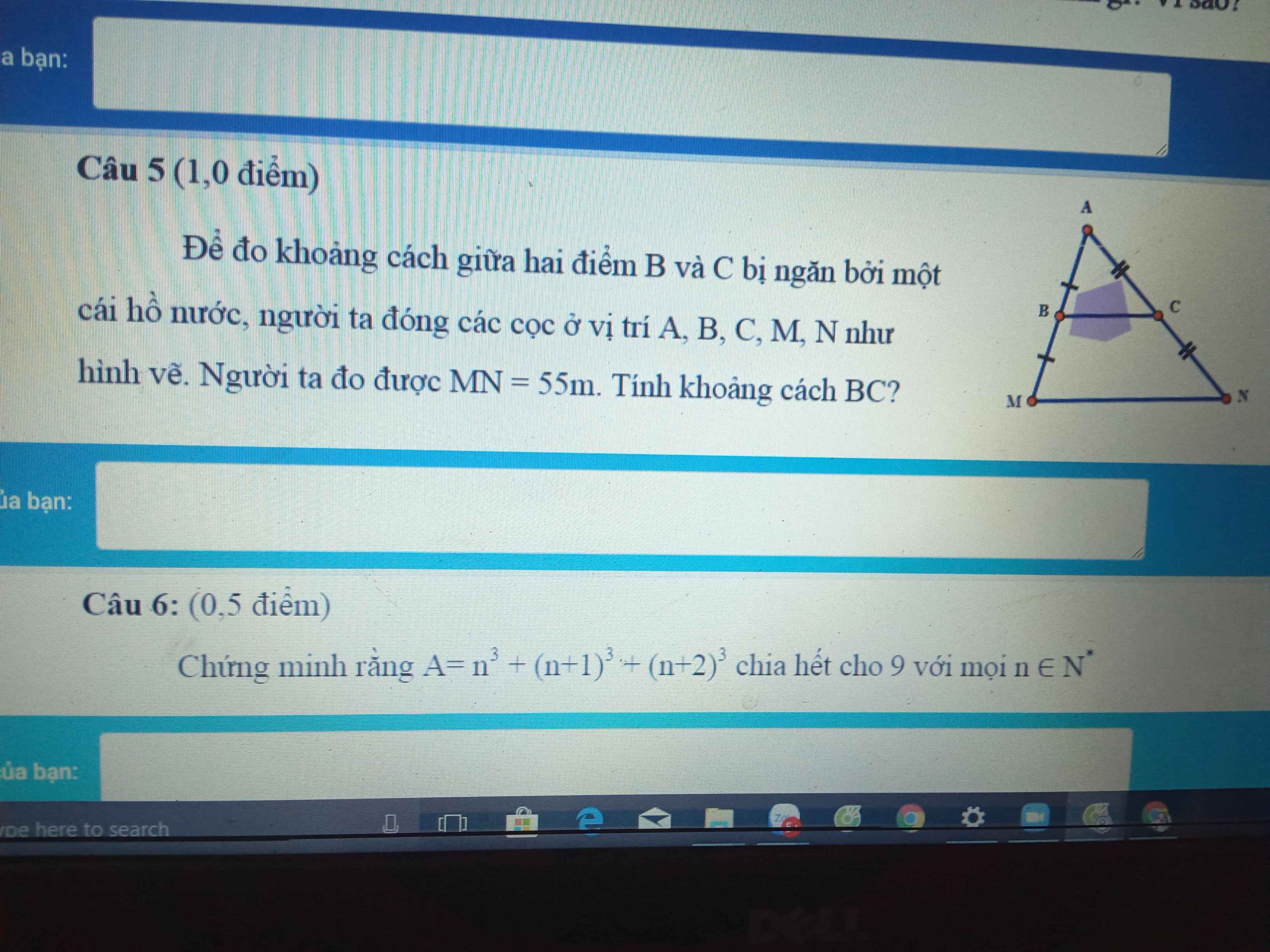
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5a.
Pt có 2 nghiệm pb lhi:
\(\Delta=9+4m>0\Leftrightarrow m>-\dfrac{9}{4}\)
b. Phương trình có 2 nghiệm khi:
\(\Delta=1+4\left(-2m+1\right)\ge0\Rightarrow m\le\dfrac{5}{8}\)
6.
a. Pt có 2 nghiệm khi:
\(\Delta'=1-\left(m+2\right)\ge0\Leftrightarrow m\le-1\)
6b
Khi \(m\le-1\), theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m+2\end{matrix}\right.\)
\(x^2_1+x^2_2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(m+2\right)=10\)
\(\Leftrightarrow m=-5\)
B.
\(x^2_1+x_2^2+4x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+2x_1x_2=0\)
\(\Leftrightarrow4+2\left(m+2\right)=0\)
\(\Leftrightarrow m=-4\)


Bài 5
\(n_{Al_2O_3}=\dfrac{10,2}{102}=0,1\left(mol\right)\)
\(n_{HCl}=\dfrac{18,25}{36,5}=0,5\left(mol\right)\)
PTHH: Al2O3 + 6HCl --> 2AlCl3 + 3H2O
Xét tỉ lệ: \(\dfrac{0,1}{1}>\dfrac{0,5}{6}\) => Al dư, HCl hết
PTHH: Al2O3 + 6HCl --> 2AlCl3 + 3H2O
\(\dfrac{1}{12}\)<----0,5------->\(\dfrac{1}{6}\)----->0,25
=> \(\left\{{}\begin{matrix}m_{Al\left(dư\right)}=10,2-\dfrac{1}{12}.102=1,7\left(g\right)\\m_{AlCl_3}=\dfrac{1}{6}.133,5=22,25\left(g\right)\\m_{H_2}=0,25.18=4,5\left(g\right)\end{matrix}\right.\)
Bài 6
a) \(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
\(n_{Mg}=\dfrac{4,8}{24}=0,2\left(mol\right)\)
PTHH: Mg + 2HCl --> MgCl2 + H2
0,1<-------------0,1<----0,1
=> \(n_{Mg\left(pư\right)}=0,1\left(mol\right)< 0,2\)
=> Mg dư => HCl hết
b) \(m_{MgCl_2}=0,1.95=9,5\left(g\right)\)
\(m_{Mg\left(dư\right)}=\left(0,2-0,1\right).24=2,4\left(g\right)\)

câu 6 thể tích 1kg khí ở 0 độ 1,29 m3
áp dụng đẳng quá trình \(\dfrac{P_0V_0}{T_0}=\dfrac{PV}{T}\Leftrightarrow\dfrac{1,01.10^5.1,29}{0+273}=\dfrac{3.10^5.V}{70+273}\Rightarrow V\approx0,5456\left(m^3\right)\)
khối lượng riêng 0,5456kg/m3


Bài 5:
a. \(\sqrt{x^2+2x+1}=\sqrt{9x^2}\)
<=> \(\sqrt{\left(x+1\right)^2}=\sqrt{\left(3x\right)^2}\)
<=> \(\left|x+1\right|=\left|3x\right|\)
<=> \(\left[{}\begin{matrix}x+1=3x\\x+1=-3x\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=0,5\\x=-0,25\end{matrix}\right.\)
b. \(\sqrt{x^2-\dfrac{2}{5}x+\dfrac{1}{25}}=\sqrt{\left(2x+1\right)^2}\)
<=> \(\sqrt{\left(x-\dfrac{1}{5}\right)^2}=\sqrt{\left(2x+1\right)^2}\)
<=> \(\left|x-\dfrac{1}{5}\right|=\left|2x+1\right|\)
<=> \(\left[{}\begin{matrix}x-\dfrac{1}{5}=2x+1\\x-\dfrac{1}{5}=-2x-1\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=-1,2\\x=-\dfrac{4}{15}\end{matrix}\right.\)
c. \(\sqrt{25x^2}=\sqrt{x^4}\)
<=> \(\sqrt{\left(5x\right)^2}=\sqrt{\left(x^2\right)^2}\)
<=> \(\left|5x\right|=\left|x^2\right|\)
<=> \(\left[{}\begin{matrix}5x=x^2\\5x=-x^2\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}5x-x^2=0\\5x+x^2=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x\left(5-x\right)=0\\x\left(5+x\right)=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}\left[{}\begin{matrix}x=0\\5-x=0\end{matrix}\right.\\\left[{}\begin{matrix}x=0\\5+x=0\end{matrix}\right.\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\\\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)










Xét tam giác AMN có:
B là trung điểm AM (gt)
C là trung điểm AN(gt)
=>BC là đường trung bình tam giác AMN
Nên: BC //MN; BC=MN/2 (tính chất ĐTB)
BC=MN/2=55/2=27,5 (m)
TỰ KẾT LUẬN