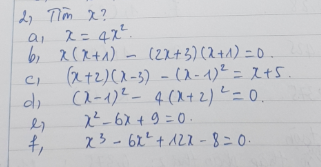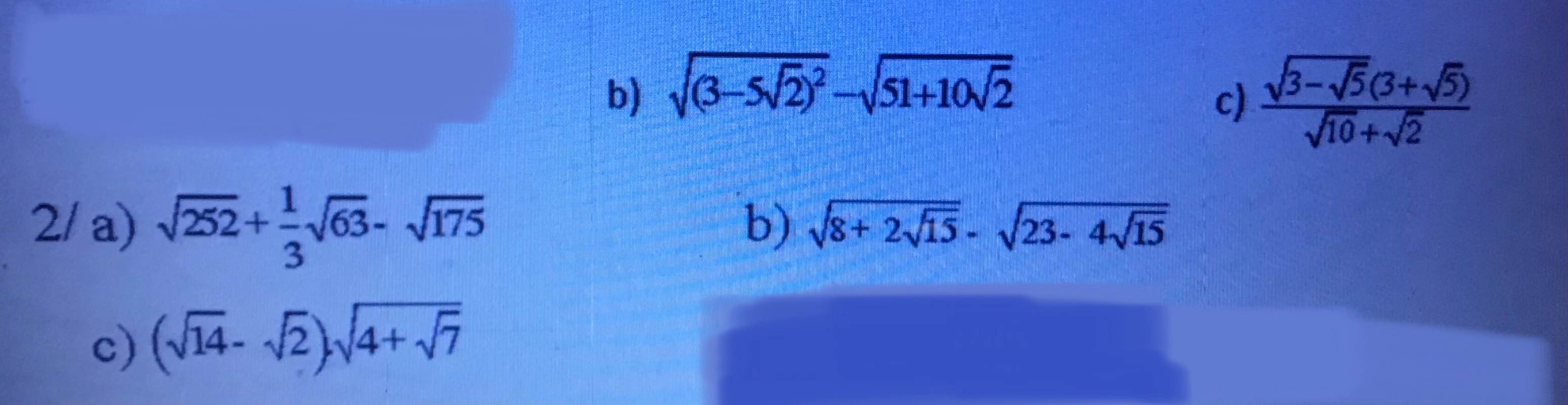Cứu ạ làm đừng có tắt nha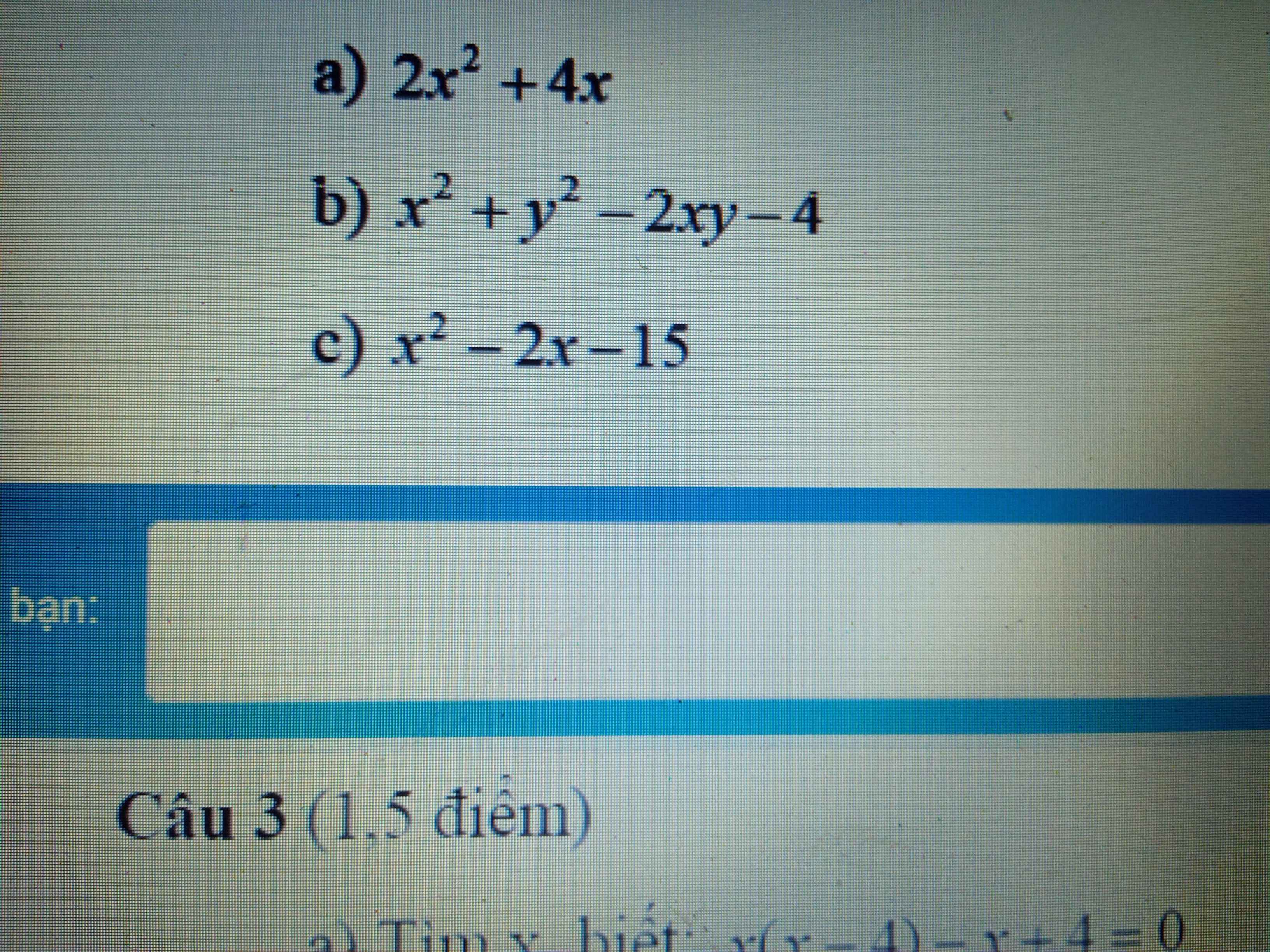
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 10 2021
b: Ta có: \(x\left(x+1\right)-\left(2x+3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-2x-3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
d: Ta có: \(\left(x-1\right)^2-4\left(x+2\right)^2=0\)
\(\Leftrightarrow\left(x-1-2x-4\right)\left(x-1+2x+4\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-1\end{matrix}\right.\)
9 tháng 2 2022
\(a,\dfrac{-2}{5}+\dfrac{4}{5}x=\dfrac{3}{5}\)
\(\Rightarrow\dfrac{4x-2}{5}=\dfrac{3}{5}\)
\(\Rightarrow4x-2=3\)
\(\Rightarrow4x=5\)
\(\Rightarrow x=\dfrac{5}{4}\)
\(b,\dfrac{-3}{7}-\dfrac{4}{7}:x=-2\)
\(\Rightarrow\dfrac{-4}{7x}=\dfrac{-11}{7}\)
\(\Rightarrow7x=\dfrac{-4.7}{-11}\)
\(\Rightarrow7x=\dfrac{28}{11}\)
\(\Rightarrow x=\dfrac{4}{11}\)
N
15 tháng 10 2021
Bài 5:
Điện trở tương đương: \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{10.10}{10+10}=5\Omega\)
Số chỉ Ampe kế: \(I=U:R=10:5=2A\)
Bài 6:
Điện trở tương đương: \(R=R1+R2=20+20=40\Omega\)
Số chỉ Ampe kế: \(I=U:R=10:20=0,5A\)
Điện trửo tương đương:
\(R'=\dfrac{\left(R3+R1\right)R2}{R3+R1+R2}=\dfrac{\left(10+20\right)20}{10+20+20}=12\Omega\)
Số chỉ Ampe kế: \(I'=U:R'=10:12=\dfrac{5}{6}A\)
12 tháng 10 2021
b: Ta có: \(\sqrt{8+2\sqrt{15}}-\sqrt{23-4\sqrt{15}}\)
\(=\sqrt{5}+\sqrt{3}-2\sqrt{5}+\sqrt{3}\)
\(=2\sqrt{3}-\sqrt{5}\)
NA
1
12 tháng 10 2021
a: \(\sqrt{252}+\dfrac{1}{3}\sqrt{63}-\sqrt{175}\)
\(=4\sqrt{7}+\sqrt{7}-5\sqrt{7}\)
=0
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 6 2021
Mình bận 1 xíu, nhưng nếu học giới hạn thì bạn cần nắm rõ các khái niệm và các dạng vô định cũng như không phải vô định đã
Giới hạn này không phải là 1 giới hạn vô định (mẫu số xác định và hữu hạn), khi gặp giới hạn kiểu này thì chỉ có 1 cách: thay số tính trực tiếp như lớp 1 là được:
\(\lim\limits_{x\rightarrow\dfrac{\pi}{2}}\dfrac{sin\left(x-\dfrac{\pi}{4}\right)}{x}=\dfrac{sin\left(\dfrac{\pi}{2}-\dfrac{\pi}{4}\right)}{\dfrac{\pi}{2}}=\dfrac{\sqrt{2}}{\pi}\)
18 tháng 10 2021
a: \(x^2-4x-5=\left(x-5\right)\left(x+1\right)\)
b: \(x^2-3x+2=\left(x-2\right)\left(x-1\right)\)
d: \(2x^2-3x+1=\left(x-1\right)\left(2x-1\right)\)
k: \(4x^2-9=\left(2x-3\right)\left(2x+3\right)\)