Tìm nguyên hàm của các hàm số f ( x ) = x 3 - 2 x + 5 thoả mãn F ( 1 ) = 3
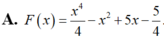
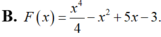
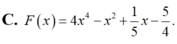
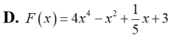
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(\left|x^4-1\right|\)\(+\left|y^2-3\right|=0\)
-Vì: $\left\{\begin{matrix}
|x^4-1|\geq 0 & \\
|y^2-3|\geq 0 &
\end{matrix}\right.$
-Để: $|x^4-1|+|y^2-3|=0$
-Thì:
$\Rightarrow \left\{\begin{matrix}
|x^4-1|=0 & \\
|y^2-3|=0 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x^4-1=0 & \\
y^2-3=0 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x^4=1 & \\
y^2=3 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=\pm 1 & \\
y=\pm \sqrt{3} &
\end{matrix}\right.$
b, Đề thiếu kìa bạn!!

Ta có f(x+1)- f(x) = 100 suy ra 5^x + 1-5^x =100 => x=2. HẾT

Chọn D
Đặt t = 8 - x 2 ⇒ t 2 = 8 - x 2 ⇒ - t d t = x d x
∫ x 8 - x 2 d x = - ∫ t d t t = - t + C = - 8 - x 2 + C
Vì F ( 2 ) = 0 nên - 8 - 4 + C = 0 suy ra C = 2.
Ta có phương trình - 8 - x 2 + 2 = x ⇔ x = 1 - 3

Chọn A
Đặt t = ln 2 x + 1 ⇒ t 2 = ln 2 x + 1 ⇒ t d t = ln x x d x
∫ ln 2 x + 1 . ln x x d x = ∫ t 2 d t = t 3 3 + C = ln 2 x + 1 3 3 + C
Vì F ( 1 ) = 1 3 nên C = 0
Vậy F 2 ( e ) = 8 9
Đáp án A.