Cho một khối cầu tâm O bán kính bằng 6cm. Mặt phẳng (P) cách O một khoảng x (cm) cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng A. 2cm B. 3cm. C. 4cm D....
Đọc tiếp
Cho một khối cầu tâm O bán kính bằng 6cm. Mặt phẳng (P) cách O một khoảng x (cm) cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng
A. 2cm
B. 3cm.
C. 4cm
D. 0cm
(
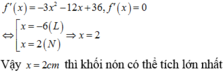
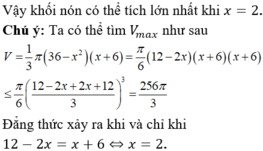
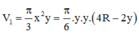
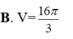
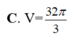
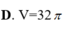
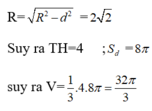
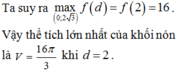
Chọn đáp án A
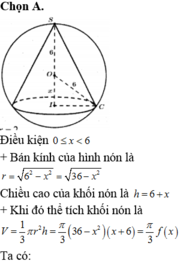
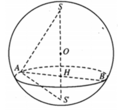
Gọi I là tâm của hình tròn (C) và S là đỉnh của hình nón. Gọi bán kính của hình tròn (C) là r thì
Trường hợp 1: O nằm giữa S và I.
Chiều cao của hình chóp là SI = SO + OI = x + 6 (cm).
Thể tích khối chóp là V = 1 3 π 36 - x 2 x + 6 cm 3
Xét hàm số f x = 36 - x 2 x + 6 với 0 ≤ x < 6
Ta có f ' x = - 3 x 2 - 12 x + 36
Do 0 ≤ x < 6 nên x = - 6.
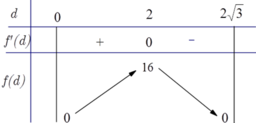
Lập bảng biến thiên của hàm số ta thấy f(x) ta thấy f x ≤ f 2 = 256
Suy ra V ≤ V 1 = 1 3 π . 256 = 256 3 π cm 3
Dấu “=” xảy ra x = 2.
Trường hợp 2: I nằm giữa S và O
Chiều cao của hình chóp là SI = SO – OI = 6 – x (cm)
Thể tích của khối chóp là V = 1 3 π 36 - x 2 6 - x cm 3 (cm3).
Xét hàm số g x = 36 - x 2 6 - x với 0 ≤ x < 6
Ta có g ' x = 3 x 2 - 12 x - 36 < 0 , ∀ x ∈ 0 ; 6 nên hàm số g(x) nghịch biến trên 0 ; 6 .
Suy ra g x ≤ g 0 = 216
Khi đó V ≤ V 2 = 72 π cm 3 .
Dấu “=” xảy ra khi x = 0.
So sánh hai trường hợp 1 và 2, suy ra thể tích lớn nhất của khối chóp đã cho là V = 256 3 π cm 3 khi x = 2 c m .