Cho hàm số
y
=
f
x
có đạo hàm trên
ℝ
và đồ thị hàm số
f
'
x
trên
ℝ
như hình vẽ. Mệnh đề nào sau đây là đúng? A. Hàm số
y
=
f
x
có 1 điểm cực tiểu và không có cực đại. B. Hàm số
y
=
f
x
có 1 điểm cực đại và không có cực tiểu. C. Hàm số
y
=
f
x
có 1 điểm cực đại và 2 điểm...
Đọc tiếp
Cho hàm số y = f x có đạo hàm trên ℝ và đồ thị hàm số f ' x trên ℝ như hình vẽ. Mệnh đề nào sau đây là đúng?
A. Hàm số y = f x có 1 điểm cực tiểu và không có cực đại.
B. Hàm số y = f x có 1 điểm cực đại và không có cực tiểu.
C. Hàm số y = f x có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số y = f x có 1 điểm cực đại và 1 điểm cực tiểu.
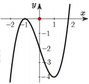
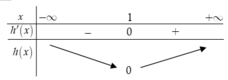
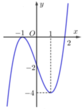
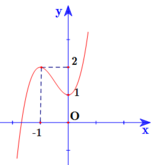
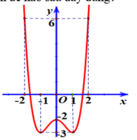
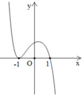
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số y = f ' x cắt trục Ox tại 1 điểm qua điểm đó hàm số y = f ' x đổi dấu từ âm sang dương nên điểm đó là điểm cực tiểu của hàm số y = f x
Chọn A.