Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
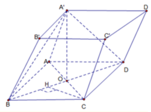
Đáp án C
Do A B ' ∩ A ' B cắt nhau tại trung điểm mỗi đường.
Do đó d B ' = d A = d C
+) Dựng C H ⊥ B D ⇒ C H ⊥ A ' B D
+) Do đó: d B ' ; A ' B D = d C ; A ' B D = C H
= B C . C D B D = a 3 2 .
Đáp án C.
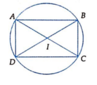
Kí hiệu như hình vẽ. Bán kính đường tròn là giao tuyến của mặt phẳng A B C D với mặt cầu đi qua 8 đỉnh của hình hộp là IA.
Ta có
I A = A C 2 = 1 2 . A B 2 + A D 2 = 1 2 b 2 + c 2
b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)
Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)
Vậy \(AC'=a\sqrt{3}\)
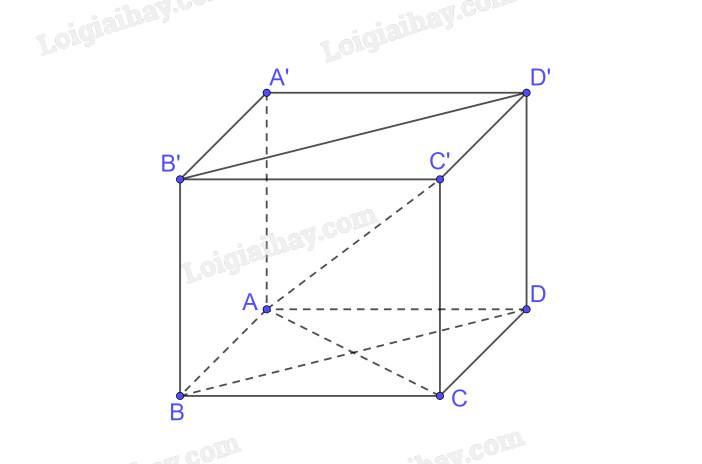
a) Ta có \(BB' \bot \left( {ABCD} \right);BB' \subset \left( {BDD'B'} \right) \Rightarrow \left( {BDD'B'} \right) \bot \left( {ABCD} \right)\)
b) A là hình chiếu của A trên (ABCD)
C là hình chiếu của C’ trên (ABCD) do \(CC' \bot \left( {ABCD} \right)\)
\( \Rightarrow \) AC là hình chiếu của AC’ trên (ABCD)
c) Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \)
Xét tam giác AC’C vuông tại C có
\(A{C'^2} = C{C'^2} + A{C^2} = {c^2} + {a^2} + {b^2} \Rightarrow A'C = \sqrt {{a^2} + {b^2} + {c^2}} \)
Đáp án C