Tính diện tích phần tô đậm, AB = FH = HE = GC = 1/2 DG và E, F là trung điểm của AD và BC. (Xem hình vẽ). Biết diện tích hình EHGD là 3cm2. Tìm diện tích hình thang ABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1:
Gọi điểm K nằm ở trung điểm DG.
Nối BH, EK, KH, FG
=> Hình thang ABCD được chia thành 8 tam giác có diện tích bằng nhau.
Mà S(EHGD) = 3cm2 ứng với 3 tam giác
=> S(ABCD) = 3:3 x 8 = 8 cm2
Cách 2: Coi độ dài cạnh AB = FH = HE = GC = a
=> DG = 2xa
Coi chiều cao của hình EHGD là h thì đường cao của hình thang ABCD là 2 x h
S(EHGD) = ( a x 2 + a) x h x 1/2 = a x 3 x h x 1/2
S(ABCD) = [ ( a x 2 + a ) + a] x h x 2 x 1/2 = a x 8 x h x 1/2
=> Tỉ số S(EHGD) / S(ABCD) = a x 3 x h x 1/2 / a x 8 x h x 1/2 = 3/8
=> S(ABCD) = 3 : 3/8 = 8 cm2

a: \(S_{AMB}=\dfrac{1}{2}\cdot6\cdot4=2\cdot6=12\left(cm^2\right)\)
\(S_{MBC}=\dfrac{1}{2}\cdot4\cdot12=2\cdot12=24\left(cm^2\right)\)
b: \(S_{ABCD}=\dfrac{1}{2}\cdot8\cdot\left(6+12\right)=4\cdot18=72\left(cm^2\right)\)

BC = 18 × 2/3 = 12 (cm)
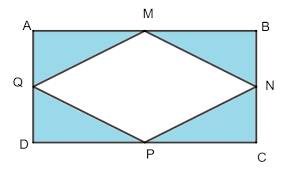
Diện tích hình thoi MNPQ:
18 × 12 : 2 = 108 (cm²)
Diện tích hình chữ nhật ABCD:
18 × 12 = 216 (cm²)
Diện tích phần tô đậm:
216 - 108 = 108 (cm²)
Gọi điểm K nằm ở trung điểm DG. Nối BH, EK, KH, FG => Hình thang ABCD được chia thành 8 tam giác có diện tích bằng nhau. Mà S(EHGD) = 3 c m 2 ứng với 3 tam giác => S(ABCD) = 3:3 x 8 = 8 c m 2