Chứng minh rằng: x 2 - x + 3 4 > 0 với mọi giá trị của x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 1 2019
Đúng(0)
Những câu hỏi liên quan
NT
1
VT
3 tháng 10 2019
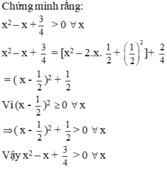
= (x2-x+1)(x2+3x+10)+10 = P
x2-x+1=(x-\(\frac{1}{2}\))2+\(\frac{3}{4}\)>0
x2+3x+10=(x+\(\frac{3}{2}\))2+\(\frac{31}{4}\)>0
vây P>0
HK
0
HP
2
29 tháng 12 2018
x^2 - x + 3/4
= x^2 - 2.x.(1/2) + (1/2)^2 - (1/2)^2 + 3/4
= (x-1/2)^2 + 1/2
Có (x-1/2)^2 >= 0 => (x-1/2)^2 + 1/2 >= 1/2 > 0
Vậy x^2 - x + 3/4 > 0 với mọi giá trị của x
29 tháng 12 2018
\(x^2-x+\frac{3}{4}=x^2-2.x.\frac{1}{2}+\frac{1}{4}+\frac{1}{2}=\left(x-\frac{1}{2}\right)^2+\frac{1}{2}\)
Do \(\left(x-\frac{1}{2}\right)^2\ge0\)
\(\left(x-\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}>0\)
\(\RightarrowĐPCM\)
NA
0
DV
0
DQ
0
TT
1
6 tháng 10 2018
Để \(B=\frac{x^2-x+1}{2}>0\forall x\) thì ta cần chứng minh :
\(x^2-x+1>0\)
\(x^2-2\cdot x\cdot\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}\)
\(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)( đpcm )
NA
6 tháng 10 2018
a) Ta có \(2x^2-8x+13=2x^2-8x+8+5\)
\(=2\left(x^2-4x+4\right)+5\)
\(=2\left(x-2\right)^2+5\ge5\forall x\)
6 tháng 10 2018
Giả sử trước khi làm nhé
\(a)\)\(2x^2-8x+13>0\)
\(\Leftrightarrow\)\(4x^2-16x+26>0\)
\(\Leftrightarrow\)\(\left(4x^2-16+16\right)+10>0\)
\(\Leftrightarrow\)\(\left(2x-4\right)^2+10\ge10>0\) ( luôn đúng )
Vậy ...
\(b)\)\(-2+2x-x^2< 0\)
\(\Leftrightarrow\)\(x^2-2x+2>0\)
\(\Leftrightarrow\)\(\left(x^2-2x+1\right)+1>0\)
\(\Leftrightarrow\)\(\left(x-1\right)^2+1\ge1>0\) ( luôn đúng )
Vậy ...
Chúc bạn học tốt ~