Cho (H) là hình phẳng giới hạn bởi Parabol: y = x 2 và đường tròn x 2 + y 2 = 2 (phần tô đậm trong hình bên). Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục hoành
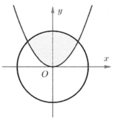
A. V = 44 π 15
B. V = 22 π 15
C. V = 5 π 3
D. V = π 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Hoành độ giao điểm của (P) và ( C) là nghiệm của 3 x 2 = 4 - x 2 <=> x = 1 hoặc x = -1
Khi đó, diện tích cần tính là H = 2x ( ∫ 0 1 4 - x 2 d x - ∫ 0 1 3 x 2 d x ) = 2 π + 3 3

Đáp án B
Xét phương trình tương giao:
3 x 2 = 4 − x 2 ⇔ 3 x 4 = 4 − x 2 ⇔ x 2 = 1 ⇒ x = ± 1 x 2 = − 4 3 ( L ) S = ∫ 0 1 3 x 2 d x + ∫ 1 2 4 − x 2 d x = 3 x 3 3 1 0 + S 2 S 2 : x = 2 sin t , t ∈ ( − π 2 ; π 2 ) ⇒ d x = 2 cos t d t S 2 : ∫ π 6 π 2 2 cos t .2 cos t d t = ∫ π 6 π 2 4 cos 2 t d t = 2 ∫ π 6 π 2 ( 1 + cos 2 t ) d t = 2 [ t + sin 2 t 2 ] π 2 π 6 = 2 π 3 − 3 2 ⇒ S = 3 3 + 2 π 3 − 3 2

Đáp án B.
Phương trình hoành độ giao điểm là:
3 x 2 = 4 − x 2 ⇒ 0 ≤ x ≤ 2 3 x 4 = 4 − x 2 ⇔ x = 1.
Dựa vào hình vẽ ta có:
S = ∫ 0 1 3 x 2 d x + ∫ 1 2 4 − x 2 d x = 3 x 3 3 1 0 + I 1 = 3 3 + I 1
Với I = ∫ 1 2 4 − x 2 d x , sử dụng CASIO
hoặc đặt x = 2 sin t ⇒ d x = 2 cos t d t
Đổi cận
x = 1 ⇒ t = π 6 x = 2 ⇒ t = π 2 ⇒ I 1 = ∫ π 6 π 2 4 − 4 sin 2 t . c o s tdt = ∫ π 6 π 2 2 1 + c o s 2 t d t = 2 t − sin 2 t π 2 π 6
⇒ I 1 = 1 6 4 π − 3 3 . Do đó S = 4 π − 3 6 .