Cho đa thức f(x) hệ số thực và thỏa điều kiện 2 f x + f 1 - x = x 2 , ∀ x ∈ ℝ . Tìm tất cả các giá trị của tham số thực m để hàm số y = 3 x . f x + m - 1 x + 1 đồng biến trên ℝ
A. m ∈ ℝ
B. m ≥ 10 3
C. m ≤ 1
D. m > 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ giả thiết, thay x bởi x-1 ta được ![]()
Khi đó ta có 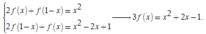
Suy ra ![]()
YCBT ![]()
![]()
Chọn B.

Đáp án C

Bảng biến thiên của hàm số f(x) là
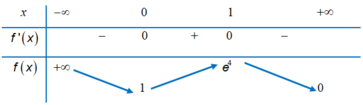
Hàm số f x là hàm số chẵn trên ℝ nên đồ thị của hàm số nhận trục tung làm trục đối xứng. Do đó phương trình f ( x ) + m = 0 có bốn nghiệm thực phân biệt khi và chỉ khi phương trình f ( x ) + m = 0 có hai nghiệm dương phân biệt hay phương trình f ( x ) = - m có hai nghiệm dương phân biệt
⇔ 1 < - m < e 4 ⇔ - e 4 < m < - 1

Đáp án C
Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức f ' x f x = 2 - 2 x *
Lấy nguyên hàm 2 vế (*), ta được ∫ d f x f x = ∫ 2 - 2 x d x
⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C
Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó f x = e - x 2 + 2 x
Xét hàm số f x = e - x 2 + 2 x trên - ∞ ; + ∞ , có f ' x = - 2 x + 2 = 0 ⇔ x = 1
Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0
Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt ⇔ 0 < m < e .

Đáp án A.
Ta có f ' ( x ) = = cos x - 2 m cos 2 x - cos 3 x + 2 m = cos x - cos 3 x - 2 m ( cos 2 x - 1 )
Hàm số có f ' ( x ) ≥ 0 , ∀ x ∈ ℝ ⇔ cos x - cos 3 x ≥ 2 m cos 2 x - 1 , ∀ x ∈ ℝ . (*)
Với cos 2 x = 1 thì thỏa mãn (*).
Với cos 2 x ≢ 1 thì ⇔ cos x - cos 3 x cos 2 x - 1 ≤ 2 m , ∀ x ∈ ℝ .
Đặt cos x - cos 3 x cos 2 x - 1 = g ( x ) . Để g ( x ) ≤ 2 m , ∀ x ∈ ℝ , thì 2 m ≥ m a x R g ( x ) .
Sử dụng máy tính cầm tay ta có
![]()
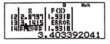
Từ bảng giá trị kết hợp với phương án thì ta suy ra
m a x ℝ g ( x ) = 2 ⇔ 2 m ≥ 2 ⇔ m ≥ 1 .