Cho tứ diện đều ABCD;M là trung điểm của cạnh BC Khi đó cosin của góc giữa hai đường thẳng nào sau đây có giá trị bằng bằng 3 6 .
A. A B ; D M
B. A D ; D M
C. A M ; D M
D. A B ; A M
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
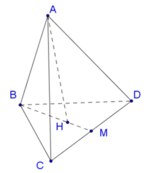
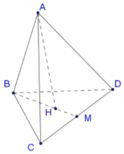
Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD.
Ta có A H ⊥ B C D (giả thiết ABCD là tứ diện đều)
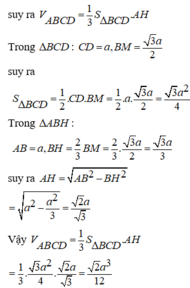

Chọn C
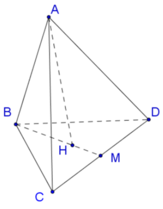
Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD

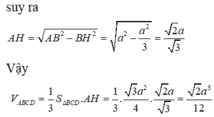

Đáp án B
Gọi M là trung điểm của CD , H là trọng tâm của tam giác BCD.
Ta có AH ⊥ BCD (giả thiết ABCD là tứ diện đều) suy ra


Đáp án C
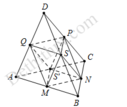
Khối bát diện đều có cạnh là a.
Chia bát diện đều thành hai hình chóp tứ giác đều có tất cả các cạnh bằng a.
Thể tích khối chóp tứ giác đều S.MNPQ là


Đáp án B
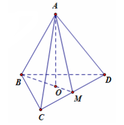
Gọi O là tâm của tam giác BCD và M là trung điểm CD
 ⇒
A
O
⊥
(
B
C
D
)
⇒
d
A
;
B
C
D
=
A
O
=
6
⇒
A
O
⊥
(
B
C
D
)
⇒
d
A
;
B
C
D
=
A
O
=
6
Đặt độ dài cạnh của tứ diện ABCD là x ⇒ B O = 2 B M 3 = x 3 3
⇒ A O = A B 2 - B O 2 = x 6 3 = 6 ⇔ x = 3 6
⇒ V = S B C D . A O 3 = x 2 3 . A O 12 = 27 3
Đáp án A
Giả sử cạnh tứ diện là a và G là trọng tâm tam giác BCD
Ta có A D ; D M ⏜ = A D M ⏜ và cos A D M ⏜ = G D A D = 3 3
A M ; D M ⏜ = A M G ⏜ , c o s A M G ⏜ = M G A M = 1 3
A B ; A M ⏜ = M A B ⏜ = 30 °
Sử dụng PP loại trừ