Cho hàm số y = f(x) xác định trên M và có đạo hàm f ' ( x ) = x 2 x - 1 2 Khẳng định nào sau đây là khẳng định đúng? A. Hà...

PT

Pham Trong Bach

3 tháng 12 2019

Cho hàm số y = f(x) xác định trên M và có đạo hàm f ' ( x ) = x + 2 x - 1 2 Khẳng định nào sau đây là khẳng định đúng? A. Hàm số đồng biến trên B. Hàm số đạt cực đại tại C. Hàm số đạt cực đại tiểu D. Hàm số nghịch biến...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

3 tháng 12 2019

Đáp án A

Đúng(0)

PT

Pham Trong Bach

12 tháng 11 2019

Cho hàm số y=f(x) xác định trên M và có đạo hàm f ' x = x + 2 x − 1 2 . Khẳng định nào sau đây là khẳng định đúng? A. Hàm số y = f(x) đồng biến trên − 2 ; + ∞ . B. Hàm số y=f(x) đạt cực đại tại x=-2 C. Hàm số đạt y=f(x) cực đại tiểu x=1 D. Hàm số y=f(x) nghịch biến trên...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

12 tháng 11 2019

Đáp án A

Ta lập bảng xét dấu của y'

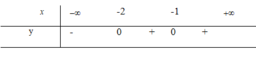
Từ bảng xét dấu trên thì hàm số đồng biến trên − 2 ; + ∞ .

Đúng(0)

PT

Pham Trong Bach

31 tháng 12 2018

Cho hàm số y=f(x) xác định trên M và có đạo hàm f ' x = x + 2 x - 1 2 Khẳng định nào sau đây là khẳng định đúng? A. Hàm số y=f(x)đồng biến trên (-2;+∞) B. Hàm số y=f(x)đạt cực đại tại x= -2 C. Hàm số y=f(x)đạt cực đại tiểu x=1 D. Hàm số y=f(x)nghịch biến trên...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

31 tháng 12 2018

Ta lập bảng xét dấu của y’

x	+∞ -2 -1 +∞
y’	- 0 + 0 +

Từ bảng xét dấu trên thì hàm số đồng biến trên (-2;+∞)

Đáp án A

Đúng(0)

PT

Pham Trong Bach

11 tháng 4 2019

Cho hàm số y= f( x) liên tục và xác định trên R. Biết f( x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ. Xét trên , khẳng định nào sau đây đúng? A. Hàm số y= f( x) đồng biến trên khoảng . B. Hàm số y= f( x) nghịch biến trên khoảng . C. Hàm số y= f(x) nghịch biến trên khoảng - π ; - π 2 và π 2 ; π . D. Hàm...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

11 tháng 4 2019

Chọn D

Trong khoảng đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)

Đúng(0)

PT

Pham Trong Bach

15 tháng 3 2017

Cho hàm số y= f( x) có đạo hàm f’(x) xác định, liên tục trên R và f’( x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng? A. Hàm số đồng biến trên ( 1; + ∞) B. Hàm số đồng biến trên (-∞;-1) và (3; + ∞) C. Hàm số nghịch biến trên (- ∞; -1) D. Hàm số đồng biến...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 3 2017

Chọn B

Trên khoảng và đồ thị hàm số f’( x) nằm phía trên trục hoành.

=> Trên khoảng ( -∞; -1) và ( 3; + ∞) thì f’( x) > 0.

=> Hàm số đồng biến trên khoảng ( -∞; -1) và ( 3; + ∞)

Đúng(0)

PT

Pham Trong Bach

9 tháng 5 2017

Cho hàm số y= f(x) liên tục và xác định trên R. Biết f( x) có đạo hàm f’( x) và hàm số y= f’( x) có đồ thị như hình vẽ, khẳng định nào sau đây đúng? A. Hàm số y= f( x) đồng biến trên R B. Hàm số y= f( x) nghịch biến trên R. C. Hàm số y= f( x) chỉ nghịch biến trên khoảng . D. Hàm số y= f( x) nghịch biến trên khoảng (0; + ∞)...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

9 tháng 5 2017

Chọn D

Trong khoảng (0 ; + ∞) đồ thị hàm số y= f’( x) nằm phía dưới trục hoành- tức là f’( x)< 0 trên khoảng đó

=> Hàm số y= f(x) nghịch biến trên khoảng

Đúng(0)

PT

Pham Trong Bach

10 tháng 12 2018

Cho hàm số y = f(x) liên tục và xác định trên R. Biết f(x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ, khẳng định nào sau đây đúng? A. Hàm số f( x) đồng biến trên R. B. Hàm số f( x) nghịch biến trên R. C. Hàm số f(x) chỉ nghịch biến trên khoảng (0; 1) . D. Hàm số f(x) đồng biến trên khoảng (0; + ∞)...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 12 2018

Chọn C

Trong khoảng ( 0; 1) đồ thị hàm số y= f’( x) nằm phía dưới trục hoành nên trên khoảng này thì f’( x)< 0.

=> hàm số f(x) nghịch biến trên khoảng (0; 1) .

Đúng(0)

PT

Pham Trong Bach

20 tháng 5 2017

Cho hàm số y = f(x) xác định và có đạo hàm y=f'(x). Đồ thị của hàm số y = f'(x) như hình dưới đây.Khẳng định nào sau đây là đúng? A. Hàm số y = f x có ba điểm cực trị. B. Hàm số y = f x đồng biến trên khoảng − ∞ ; 2 C. Hàm số y = f x nghịch biến trên khoảng 0 ; 1 D. Hàm số y = f ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

20 tháng 5 2017

Đáp án A

Phương pháp: Quan sát đồ thị hàm số y = f ' x để tìm khoảng dương, âm của f ' x , từ đó tìm được khoảng đồng biến, nghịch biến của f x .

Cách giải:

Từ đồ thị hàm số y = f ' x suy ra hàm số y = f x nghịch biến trên − ∞ − 1 và 1 ; 2 (làm y'âm) và đồng biến trên − 1 ; 1 (làm y'dương).

Suy ra B, C, D sai và A đúng.

Chú ý khi giải:

HS có thể nhầm lẫn thành đồ thị hàm số y = f x do đọc không kĩ đề dẫn đến chọn sai đáp án.

Đúng(0)

PT

Pham Trong Bach

23 tháng 5 2019

Hàm số y = f(x) xác định, liên tục trên khoảng K và có đạo hàm f’(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f’(x) trên K Khẳng định nào sau đây là đúng? A. Đồ thị hàm số y = f(x) đạt cực tiểu tại x = -2 B. Đồ thị hàm số y = f(x) có 2 điểm cực trị C. Hàm số y = f(x) đạt cực đại tại x = 1 D. Hàm số y = f(x) đạt giá trị lớn nhất tại x =...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

23 tháng 5 2019

Đáp án C

Từ đồ thị hàm số g = f’(x) ta thấy: hàm số f’(x) = 0 tại 2 điểm phân biệt x = -2 và x = 1

Mặt khác, tại x = 1 thì f’(x) đổi dấu từ dương sang âm, do đó hàm số y = f(x) đạt cực đại tại x = 1

Đúng(0)

PT

Pham Trong Bach

17 tháng 7 2017

Cho hàm số y=f(x) xác định và có đạo hàm f’(x). Đồ thị của hàm số f’(x) như hình vẽ bên. Khẳng định nào sau đây là đúng? A. Hàm số y=f(x) đạt cực đại tại x=5 B. Hàm số y=f(x) có bốn cực trị C. Hàm số y=f(x) đồng biến trên khoảng (-∞;1) D. Hàm số y=f(x) đạt cực tiểu tại...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

17 tháng 7 2017

Chọn D

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP