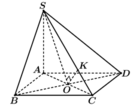
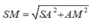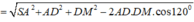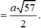Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng 3 a , B A D ^ = 60 o ,SA vuông góc với mặt đáy, góc giữa đường thẳng SC và mặt đáy bằng 45 o Gọi M,N lần lượt là trung điểm các cạnh CD và AB Khoảng cách từ điểm B đến mặt phẳng (SMN) bằng

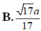
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

a: (SB;(ABCD))=(BS;BA)=góc SBA
b: (SO;(ABCD))=(OS;OA)=góc SOA
c: (SC;(SAD))=(SC;SD)


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
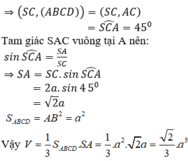

Chọn A.
Góc giữa SC và mặt đáy bằng 45 o ⇒ S C A ^ = 45 o
Xét tam giác SAC vuông tại A, ta có
![]()
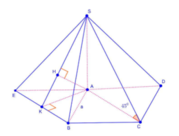
Dựng hình bình hành ACBE
![]()
Gọi H là hình chiếu của A lên mặt phẳng (SBE).
![]()
![]()
Xét hình tứ diện vuông SABE có
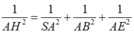
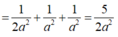
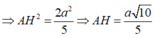

Trong tam giác SOC, kẻ OK ⊥ OS(như hình vẽ).(1)
Dễ dàng chứng minh được ![]()
![]()
![]()
Ta tính được 
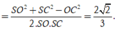
Chọn B.
Chọn C
Ta có
Do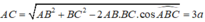
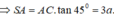
Có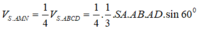
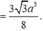
Ta lại có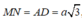
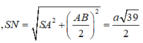
Và