Tìm các giá trị của m để đồ thị hàm số y=(x+1)(x-2)(x-m) có hai điểm cực trị thuộc về hai phía Ox.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C.
Ta có y ' = 3 x 2 - 2 ( m + 1 ) x + m 2 - 2
trước tiên ta phải có phương trình y ' = 0 có hai nghiệm phân biệt
![]()
![]()
Điều kiện hai điểm cực trị của đồ thị hàm số nằm cùng về một phía đối với trục hoành là y x 1 . y x 2 > 0
⇔ y = 0 có đúng một nghiệm thực.
Thử trực tiếp các giá trị của m∈{−1,0,1,2} nhận các giá trị m∈{−1,0,2} để y = 0 có đúng một nghiệm thực.

Chọn đáp án B
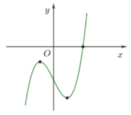
Hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành là nghiệm của phương trình :
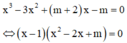
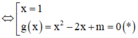
Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục hoành
Phương trình (*) có hai nghiệm phân biệt khác 1
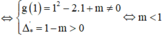

Đáp án C
TXĐ: D = ℝ .
Ta có y ' = x 2 − 2 m − 1 x + m − 1 .
Để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục tung thì
m − 1 2 − m − 1 > 0 m − 1 > 0 2 m − 1 > 0 ⇔ m > 2.
Vậy m>2 thỏa mãn điều kiện đề bài.

Chọn A
Ta có ![]() .
.
Giải phương trình 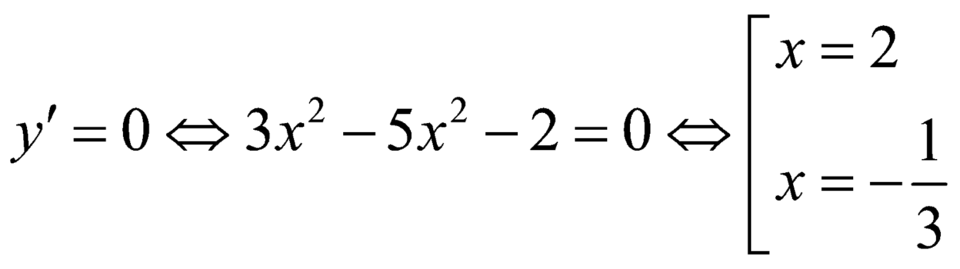 .
.
Với ![]() thì
thì ![]() .
.
Với ![]() thì
thì ![]() .
.
Hàm số có giá trị cực đại và giá trị cực tiểu trái dấu khi
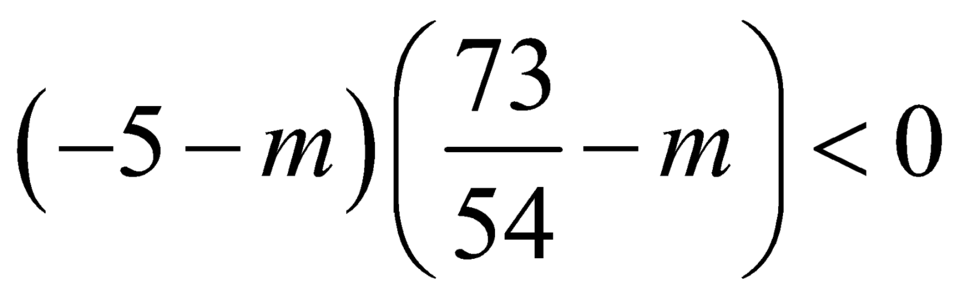
![]() .
.
Do ![]() nên
nên ![]() .
.
Vậy có 6 giá trị nguyên của m thỏa mãn.



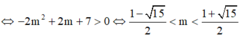
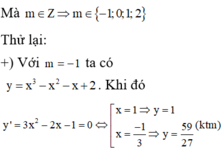
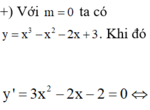
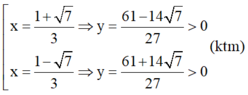
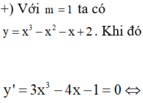
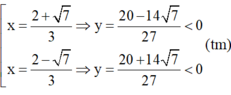
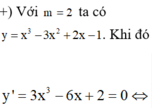
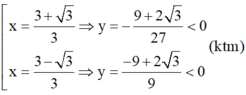



Chọn D