Giúp mik bài 3 với ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
31 tháng 10 2023
Bài 1
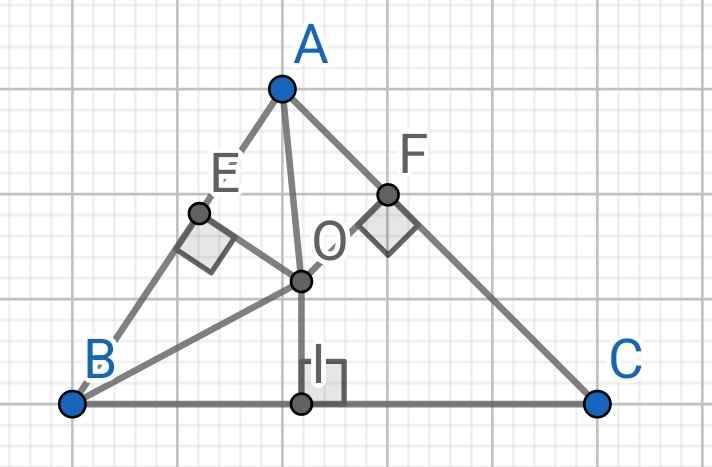Do BO là tia phân giác của ∠ABC (gt)
⇒ ∠OBE = ∠OBI
Do AO là tia phân giác của ∠BAC (gt)
⇒ ∠OAE = ∠OAF
Xét hai tam giác vuông: ∆OAE và ∆OAF có:
OA chung
∠OAE = ∠OAF (cmt)
⇒ ∆OAE = ∆OAF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng) (1)
Xét hai tam giác vuông: ∆OBE và ∆OBI có:
OB chung
∠OBE = ∠OBI (cmt)
⇒ ∆OBE = ∆OBI (cạnh huyền - góc nhọn)
⇒ OE = OI (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OE = OF = OI
KV
31 tháng 10 2023
Bài 2
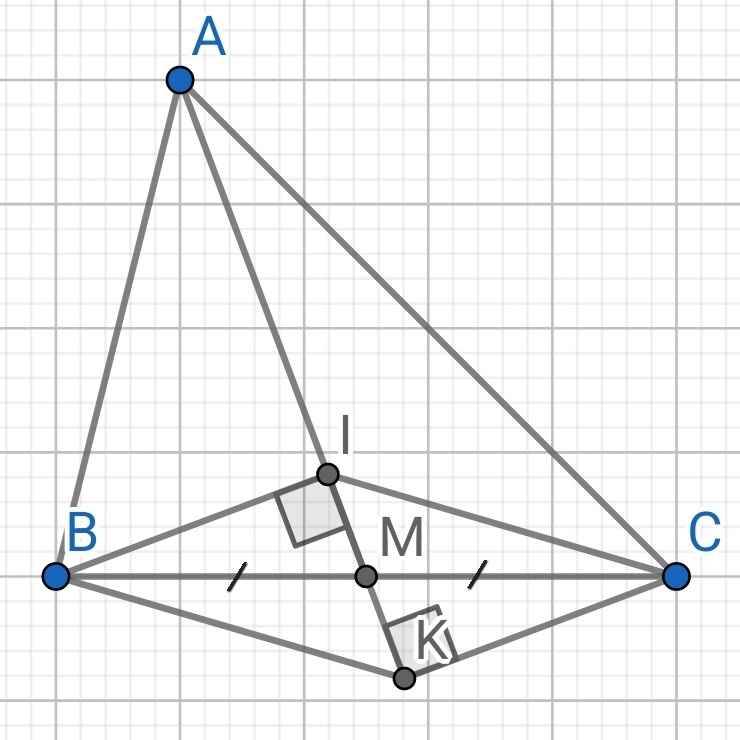a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
BM = CM (gt)
∠BMI = ∠CMK (đối đỉnh)
⇒ ∆BMI = ∆CMK (cạnh huyền - góc nhọn)
⇒ BI = CK (hai canhk tương ứn
b) Do ∆BMI = ∆CMK (cmt)
⇒ MI = MK (hai cạnh tương ứng)
Xét ∆BMK và ∆CMI có:
MK = MI (cmt)
∠BMK = ∠CMI (đối đỉnh)
BM = CM (gt)
⇒ ∆BMK = ∆CMI (c-g-c)
⇒ ∠MBK = ∠MCI (hai góc tương ứng)
Mà ∠MBK và ∠MCI là hai góc so le trong)
⇒ BK // CI
HN
13 tháng 10 2021
Câu 1: Hiện tượng: Sủi bọt khí. Giải thích: H+ kết hợp CO32- tạo ra axit yếu H2CO3 tiếp tục phân hủy thành nước và CO2 (thoát ra ngoài).
PTHH: CaCO3(r) + 2CH3COOH(dd) → Ca(CH3COO)2(dd) + H2O(l) + CO2(k)
Câu 2: Số mol muối (CH3COONa) là 0,2 bằng số mol axit axetic, m = 0,2.60 = 12 (g).
Câu 3: Số mol CO2 là 0,18; số mol nước là 0,33. Ta có: (n\(CO_2\) - n\(H_2O\)) = (\(\overline{k}\) - 1).nancol \(\Rightarrow\) Số mol hỗn hợp ancol là 0,15 (ancol no, đơn chức \(\overline{k}\)=0)
Áp dụng định luật bảo toàn nguyên tố O tìm được số mol O2 là 0,5(2.0,18 + 0,33 - 0,15) = 0,27.
Áp dụng định luật bảo toàn khối lượng tìm được khối lượng hỗn hợp ancol là 0,18.44 + 5,94 - 0,27.32 = 5,22 (g).
Khối lượng mol trung bình của hỗn hợp ancol là:
32 g/mol (CH3OH) < \(\overline{M}\)=5,22/0,15=34,8 (g/mol) < 46 g/mol (C2H5OH).
Vậy hai ancol cần tìm là CH3OH và C2H5OH.
MM
4
29 tháng 12 2021
b: Xét tứ giác ABCK có
M là trung điểm của AC
M là trung điểm của BK
Do đó: ABCK là hình bình hành
Suy ra: BC=AK
Y
19 tháng 6 2023
\(53,\sqrt{\left(a-2b\right)^2}\left(a\le2b\right)\)
\(=\left|a-2b\right|=-a+2b\)
\(54,\sqrt{4x^2-4xy+y^2}\left(2x\ge y\right)\)
\(=\sqrt{\left(2x-y\right)^2}=\left|2x-y\right|=2x-y\)
\(55,\sqrt{\left(2x-1\right)^2}\left(x\ge\dfrac{1}{2}\right)\)
\(=\left|2x-1\right|=2x-1\)
\(56,\sqrt{\left(3a-2\right)^2}\left(3a\le2\right)\)
\(=\left|3a-2\right|=-3a+2\)
\(57,\sqrt{\left(6-9x\right)^2}\left(3x\ge2\right)\)
\(=\left|6-9x\right|=-6+9x\)
\(58,\sqrt{25a^2-10a+1}\left(5a\le1\right)\)
\(=\sqrt{\left(5a-1\right)^2}=\left|5a-1\right|=-5a+1\)
\(59,\sqrt{m^2+4mn+4n^2}\left(m\ge-2n\right)\)
\(=\sqrt{\left(m+2n\right)^2}=\left|m+2n\right|=m+2n\)
\(60,\sqrt{9x^2-24xy+16y^2}\left(3x\le4y\right)\)
\(=\sqrt{\left(3x-4y\right)^2}=\left|3x-4y\right|=-3x+4y\)
H9
HT.Phong (9A5)
CTVHS
19 tháng 6 2023
Bài 3:
53. \(\sqrt{\left(a-2b\right)^2}=\left|a-2b\right|=2b-a\)
54. \(\sqrt{4x^2-4xy+y^2}=\sqrt{\left(2x-y\right)^2}=\left|2x-y\right|=2x-y\)
55. \(\sqrt{\left(2x-1\right)^2}=\left|2x-1\right|=2x-1\)
56. \(\sqrt{\left(3a-2\right)^2}=\left|3a-2\right|=2-3a\)
57. \(\sqrt{\left(6-9x\right)^2}=\left|6-9x\right|=6-9x\)
58. \(\sqrt{25a^2-10a+1}=\sqrt{\left(5a-1\right)^2}=\left|5a-1\right|=1-5a\)
59. \(\sqrt{m^2+4mn+4n^2}=\sqrt{\left(m+2n\right)^2}=\left|m+2n\right|=m+2n\)
60. \(\sqrt{9x^2-24xy+16y^2}=\sqrt{\left(3x-4y\right)^2}=\left|3x-4y\right|=4y-3x\)
Gọi A là giao điểm của (d) với (d1)
\(\Rightarrow\) Tọa độ A thỏa mãn: \(\left\{{}\begin{matrix}y=-x+2\\y=3x+1\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{1}{4};\dfrac{7}{4}\right)\)
Thay tọa độ A vào pt (d2) ta được:
\(\dfrac{7}{4}=2.\dfrac{1}{4}+2\Rightarrow\dfrac{7}{4}=\dfrac{5}{2}\) (ko thỏa mãn)
Vậy 3 đường thẳng nói trên ko đồng quy (đề bài sai)