Cho AB=AC , BD=CD chứng minh
a,tam giác ABD=ACD
b,ADB=30 độ . Tính ADC
c,AD là tia phân giác của BAC?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2022
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
b: Ta có: ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao
17 tháng 6 2023
a: Xét ΔADB và ΔADE có
AD chung
góc BAD=góc EAD
AB=AE
=>ΔADB=ΔADE
=>góc ABD=góc AED
b: Xét ΔAEF vuông tại A và ΔABC vuông tại A có
AE=AB
góc AEF=góc ABC
=>ΔAEF=ΔABC
=>AC=AF
15 tháng 2 2018
tìm một số biết rằng số đó nhân với 3 thì được số lớn nhất có một chữ số.
CM
17 tháng 7 2018
Áp dụng tính chất đường phân giác của tam giác ABC ta có:
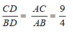
Chọn đáp án B
CM
2 tháng 4 2017
Theo tính chất tia phân giác của góc ta có:
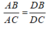
Suy ra:
Chọn đáp án D
27 tháng 6 2021
b) Xét ΔADB vuông tại D và ΔEDC vuông tại D có
DB=DC(cmt)
DA=DE(gt)
Do đó: ΔADB=ΔEDC(hai cạnh góc vuông)
Suy ra: AB=EC(Hai cạnh tương ứng)
mà AB=AC(ΔBAC cân tại A)
nên CA=CE
Xét ΔCAE có CA=CE(cmt)
nên ΔCAE cân tại C(Định nghĩa tam giác cân)